درگاه:ریاضیات
درگاههای ویکیپدیا: فرهنگ · جغرافیا · بهداشت و درمان · تاریخ · ریاضیات · علوم طبیعی · مردم · فلسفه · دین · اجتماعی · فناوری
|
درگاه ریاضیات ریاضیات (Mathematics) را معمولاً دانش بررسی کمیتها و ساختارها و فضا و تبدیل تعریف میکنند. دیدگاه دیگری ریاضی را دانشی میداند که در آن با استدلال منطقی از اصول و تعریفها به نتایج دقیق و جدیدی میرسیم. دیدگاههای دیگری نیز در فلسفه ریاضیات بیان شدهاست. اگرچه ریاضیات خود یکی از علوم طبیعی بهشمار نمیرود ولی ساختارهای ویژهای که ریاضیدانان میپژوهند، بیشتر از دانشهای طبیعی به ویژه فیزیک سرچشمه میگیرند و در فضایی جدا از طبیعت و محضگونه گسترش پیدا میکند به طوری که علوم طبیعی برای حل مسائل خود به ریاضی باز میگردند تا جوابشان را با آن مقایسه و بررسی کنند. علوم طبیعی، مهندسی و اقتصاد، بسیار به ریاضیات تکیه دارند. آن بخش از ریاضیات را که علوم کاربردی به آن بیشتر میپردازند، ریاضیات کاربردی مینامند. ولی گاه ریاضیدانان به دلایل صرفاً ریاضی و نه کاربردی به تعریف و بررسی برخی ساختارها میپردازند که به آن ریاضیات محض گفته میشود. نوشتار برگزیده نظریهٔ مجموعهها شالودهٔ بنیادین و سنگ اساسی بنای ریاضیات جدید است. تعریفهای دقیق جمیع مفاهیم ریاضی، مبتنی بر نظریهٔ مجموعههاست. گذشته از این، روشهای استنتاج ریاضی با استفاده از ترکیبی از استدلالهای منطقی و مجموعه- نظری تنظیم شدهاند. زبان نظریهٔ مجموعهها، زبان مشترکی است که ریاضیدانان در سراسر دنیا با آن صحبت کرده و آن را درک میکنند. چنان که اگر کسی بخواهد پیشرفتی در ریاضیات عالی یا کاربردهای عملی آن داشته باشد، باید با مفاهیم اساسی و زبان نظریهٔ مجموعهها آشنا شود. نظریه مجموعهها در اواخر قرن نوزدهم به طور عمده توسط جرج کانتور بنیان گذاشته شد. زندگینامهٔ برگزیده آیزاک نیوتن فیزیکدان، ریاضیدان، ستاره شناس، فیلسوف و شهروند انگلستان بودهاست. وی در سال ۱۶۸۷ میلادی شاهکار خود «اصول ریاضی فلسفه طبیعی» را به نگارش درآورد. در این کتاب او مفهوم گرانش عمومی را مطرح ساخت و با تشریح قوانین حرکت اجسام، علم مکانیک کلاسیک را پایه گذاشت. از دیگر کارهای مهم او بنیانگذاری حساب دیفرانسیل و انتگرال است. نام نیوتن با انقلاب علمی در اروپا و ارتقای نظریهٔ خورشید-مرکزی پیوند خوردهاست. او نخستین کسی است که قواعد طبیعی حاکم بر گردشهای زمینی و آسمانی را کشف کرد. مفاهیم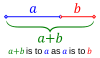 نسبت طلایی در ریاضیات و هنر هنگامی است که «نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر» باشد. تعریف دیگر نسبت طلایی این است که «عددی مثبت است که اگر به آن یک واحد اضافه کنیم به مربع آن خواهیم رسید».تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد. نوشتارهای برگزیدهنگارهٔ برگزیده در هندسه اقلیدسی، تجانس یکنواخت یا تجانس همسانگرد، تبدیلی خطی است که اشکال را در تمام جهات به یک مقیاس بزرگ یا کوچک میکند. در حالت کلیتر، ضریب تجانس در جهات گوناگون میتواند متفاوت باشد. در این صورت به آن تجانس غیریکنواخت یا ناهمسانگرد گویند.سطح زیرین گنبد مسجد شیخ لطفالله نمونه ای از تجانس است. گفتاورد«هر نوع علمی، اگر به درجه ای از بلوغ برسد، به صورت خودکار قسمتی از ریاضیات می گردد.» هندسه مثلث شکل مسطحی است که از اتصال سه نقطه غیرهمخط در صفحه به وجود میآید. مثلث دارای سه ضلع و سه زاویه است.مساحت یک مثلث برابر یک دوم طول یک ضلع، ضرب در طول ارتفاع وارد بر آن، یعنی فاصله رأس سوم تا خط شامل ضلع انتخابشده، است. مساحت مثلث را از رابطه زیر به دست میآورند:
آیا میدانستید؟ ... که یک هفتضلعی منتظم، یک چند ضلعی منتظم با کمترین اضلاع ممکن است که می توان آن را با خط کش و پرگار ساخت؟
|














