نظریه مجموعه‌ها

نظریه مجموعه‌ها (به انگلیسی: Set theory) شاخه‌ای از منطق ریاضی است که به مطالعه مجموعه‌ها می‌پردازد. مجموعه‌ها، گردایه‌ای از اشیاء هستند. هر چند هر نوعی از اشیاء می‌توانند یک مجموعه را تشکیل دهند، اما نظریه مجموعه‌ها اغلب در مورد اشیاء مرتبط با ریاضی به کار می‌رود. زبان نظریه مجموعه‌ها را می‌توان در تعریف تقریباً همه‌ی اشیاء ریاضی به کار برد. مطالعه جدید بر روی نظریه مجموعه‌ها توسط جرج کانتور و ریچارد ددکیند در دهه ۷۰ قرن ۱۸ میلادی شروع شد. پس از کشف تناقض‌های نظریه طبیعی مجموعه‌ها، دستگاه‌های اصل موضوعی بی‌شماری در اوایل قرن ۲۰ مطرح شدند که معروف‌ترین آن‌ها اصل موضوعه زرملو-فرانکل و اصل موضوعه انتخاب هستند. نظریه مجموعه‌ها عموماً به عنوان سیستم بنیادین ریاضیات در شکل نظریه مجموعه‌های زرملو-فرانکل همراه با اصل موضوعه انتخاب به کار می‌رود. ورای نقش بنیادین آن، نظریه مجموعه‌ها در جایگاه خود یکی از شاخه‌های ریاضی با جامعه پژوهش فعالی محسوب می‌شود. پژوهش‌های معاصر در نظریه مجموعه‌ها موضوع‌های متنوعی را شامل می‌شود که از ساختار خط اعداد حقیقی تا مطالعه سازگاری اعداد بزرگ متغیر است.

یک نمودار ون که اشتراک دو مجموعه را نشان می‌دهد.

تاریخچه

جرج کانتور

مباحث ریاضی به‌طور معمول از ارتباط متقابل میان پژوهش گران زیادی به دست می‌آیند. نظریه مجموعه‌ها، هرچند، با یک تک مقاله «یک خاصیت مشخصه‌ای تمام اعداد جبری حقیقی» در سال ۱۸۷۴ توسط جرج کانتور پایه‌ریزی شد. از قرن ۵ قبل از میلاد، از زمان ریاضیدان یونانی زنون الئایی در غرب و ریاضیدانان هندی در شرق، ریاضیدانان با مفهوم بی‌نهایت در کشمکش بوده‌اند. به‌خصوص یکی از کارهای قابل توجه کار برنارد بولتزانو در نیمه اول قرن ۱۹ است. درک مدرن از بی‌نهایت با کار کانتور روی نظریه اعداد در ۱۸۷۱–۱۸۶۷ شروع شد. یک ملاقات بین کانتور و ریچارد ددکیند در سال ۱۸۷۲ تفکر کانتور را تحت تأثیر قرار داد و در مقاله ۱۸۷۴ کانتور به اوج خود رسید. کار کانتور به دو قطبی شدن ریاضیدانان آن زمان انجامید. در حالی کارل وایرشتراس و ددکیند از کانتور حمایت می‌کردند، لئوپولد کرونکر، که امروزه به عنوان بنیان‌گذار ریاضیات برساخت گرایی از او یاد می‌شود، حمایت نمی‌کرد. نظریه اعداد کانتور سرانجام به علت کاربرد مفاهیم کانتوری مانند تناظرات یک به یک بین مجموعه‌ها، اثباتش مبنی بر اینکه تعداد اعداد حقیقی بیشتر از اعداد صحیح است، و «بی‌نهایت بودن بی‌نهایت‌ها» («بهشت کانتور») مبتنی بر عملکرد مجموعه توانی متداول گشت. کاربرد نظریه مجموعه‌ها منجر به ارائه مقاله «نظریه مجموعه‌ها» (به آلمانی: Mengenlehre) در سال ۱۸۹۸ از جانب آرتور شونفلایس به دائرةالمعارف کلین شد. موج جالب توجه بعدی در نظریه مجموعه‌ها حدود ۱۹۰۰ پدیدار شد، وقتی معلوم شد نظریه کانتوری مجموعه‌ها منجر به ایجاد تناقضات بسیاری شد که آنتنومیها یا پارادوکس‌ها خوانده می‌شوند. برتراند راسل و ارنست زرملو به‌طور جدا ساده‌ترین و معروف‌ترین پارادوکس را که امروزه پارادوکس راسل خوانده می‌شود پیدا کردند: «مجموعه تمام مجموعه‌هایی که عضو خودشان نیستند» را در نظر بگیرید، که منجر به این تناقض می‌شود که باید عضو خودش باشد و عضو خودش نباشد. در ۱۸۹۹ کانتور خودش را در معرض این سؤال قرار داد: «کاردینال مجموعه تمام مجموعه‌ها چقدر است؟»، و به تناقض مرتبطی رسید. راسل از پارادوکس خود در سال ۱۹۰۳ به عنوان زمینه خلاصه ریاضیات قاره‌ای در «اصول ریاضیات» اش استفاده کرد. پیشرفت نظریه مجموعه‌ها طوری بود که مناظره بر روی پارادوکس‌ها باعث رها کردن آن نشد. کار زرملو در ۱۹۰۸ و آبراهام فرانکل در ۱۹۲۲ مجموعه اصول موضوعه ZFC را نتیجه داد، که به مورد استفاده‌ترین اصول موضوعه برای نطریه مجموعه‌ها بدل شد. کار آنالیست‌هایی مثل هنری لبگ کاربرد بزرگ ریاضی نظریه مجموعه‌ها را که از آن زمان به بعد در تار و پود ریاضیات مدرن بافته شده، نشان داد. نظریه مجموعه‌ها به‌طور معمول به عنوان یک سیستم پایه استفاده می‌شود، هرچند در برخی از نواحی نظریه رده‌ها به عنوان سیستم پایه ترجیح داده می‌شود.

مفاهیم و نمادهای اصلی

مقاله‌های اصلی: مجموعه‌ها (ریاضیات) و جبر مجموعه ها

نظریه مجموعه‌ها با یک رابطه دودویی اصلی بین یک شی o و یک مجموعه A آغاز می‌شود. اگر o یک عضو (یا «عنصر») A باشد، بنویسید o ∈ A. چون مجموعه‌ها خود اشیاء هستند، رابطه عضویت نیز می‌تواند مرتبط باشد. یک رابطه دودویی برگرفته بین مجموعه‌ها رابطه زیرمجموعه‌ای است، که شمول مجموعه ای نیز نامیده می‌شود. اگر همه اعضای A اعضای B نیز باشند، A زیر مجموعه B است، که A ⊆ B نمادگذاری می‌شود. برای مثال، ‏{۱، ۲}‎ یک زیر مجموعه ‏{۱، ۲، ۳}‎ است. اما ‏{۱، ۴}‎ نیست. با این تعریف، واضح است که هر مجموعه زیر مجموعه خودش است؛ در صورتی که نخواهیم این مورد را به حساب بیاوریم، عبارت «زیرمجموعه سره» تعریف شده‌است. A زیر مجموعه سره B است اگر و فقط اگر A زیر مجموعه B باشد ولی B زیر مجموعه A نباشد. همانند حسابان که عملیات دودویی را روی اعداد پیاده‌سازی می‌کند، نظریه مجموعه‌ها نیز عملیات دودویی را روی مجموعه‌ها اعمال می‌کند.

• اجتماع مجموعه‌های A و B، مجموعه A ∪ B، مجموعه تمام اشیایی است که یا عضو A هستند، یا عضو B یا عضو هردو. اجتماع ‏{۱، ۲، ۳}‎ و ‏{۲، ۳، ۴}‎ مجموعه ‏{۱، ۲، ۳، ۴}‎ است.
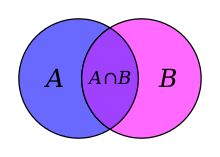
• اشتراک مجموعه‌های A و B، مجموعه A ∩ B مجموعه تمام اشیایی است که هم عضو A و هم عضو B هستند. اشتراک ‏{۱، ۲، ۳}‎ و ‏{۲، ۳، ۴}‎ مجموعه ‏{۲، ۳}‎ است.
• تفاضل مجموعه‌های U و A، مجموعه U \ A، مجموعه تمام اعضایی است که عضو U هستند ولی عضو A نیستند. تفاضل ‏{۱، ۲، ۳}‎ \ ‏{۲، ۳، ۴}‎ مجموعه ‏{۱}‎ است؛ و برعکس تفاضل ‏{۲، ۳، ۴}‎ \ ‏{۱، ۲، ۳}‎ مجموعه ‏{۴}‎ است. وقتی که A زیر مجموعه U است، تفاضل U \ A متمم A در U نیز خوانده می‌شود. در این مورد، اگر انتخاب U از متن معلوم باشد، نماد A^c بعضی اوقات به جای U \ A استفاده می‌شود، مخصوصاً وقتی U مانند مطالعه نمودار ون مجموعه جهانی باشد.
• تفاضل متقارن مجموعه‌های A و B، مجموعه A △ B یا A ⊖ B، مجموعه تمام اشیایی است که عضو دقیقاً یکی از مجموعه‌های A و B باشد. (اعضایی که در یکی از مجموعه‌ها هستند، نه در هر دو). برای مثال، برای مجموعه‌های ‏{۱، ۲، ۳}‎ و ‏{۲، ۳، ۴}‎، تفاضل متقارن مجموعه ‏{۱، ۴}‎ است. تفاضل اجتماع و اشتراک (A ∪ B) \ (A ∩ B) یا (A \ B) ∪ (B \ A) نیز همان تفاضل متقارن است.
• ضرب دکارتی A و B، مجموعه A × B مجموعه‌ای است که اعضایش تمام زوج مرتب‌های ممکن (a,b) است که a عضوی از A و b عضوی از B است. ضرب دکارتی {۱, ۲} و {red, white} می‌شود {(red,1), (red, 2), (white, 2), (white, ۱)}.
• مجموعه توانی یک مجموعه A مجموعه تمام زیر مجموعه‌های A است. برای مثال مجموعه توانی ‏{۱، ۲}‎ مجموعه ‏{{}، {۱}، {۲}، {۱، ۲}}‎ است.

برخی از مجموعه‌هایی که در کانون اهمیت قرار دارند، مجموعه تهی، مجموعه اعداد طبیعی و مجموعه اعداد حقیقی هستند.

مقداری هستی‌شناسی

مقالهٔ اصلی: جهان فون نویمان

یک بخش اولیه از سلسله مراتب فون نویمان.

یک مجموعه هنگامی محض است که همه اعضایش مجموعه باشند، و همهٔ اعضای اعضایش مجموعه باشند و به همین ترتیب … برای مثال، مجموعه که تنها مجموعه تهی را دربردارد یک مجموعه خالص ناتهی است. در نظریه مدرن مجموعه‌ها، معمول است که توجه را به جهان فون نویمان مجموعه‌های خالص معطوف کرد، و تعداد زیادی از سیستم‌های نظریه اصل موضوعی مجموعه‌ها طراحی شده‌اند که تنها مجموعه‌های خالص را اصل بندی کنند. این محدودیت از نظر فنی امتیازهای زیادی به همراه دارد و به کلیت خیلی کم لطمه می‌زند، زیرا به طرز ویژه‌ای همه مفاهیم ریاضی می‌توانند با استفاده از مجموعه‌های خالص بازسازی شوند. مجموعه‌ها در جهان ون نویمان با توجه به این که چقدر عمیق اعضایشان، اعضای اعضایشان و… در هم قرار گرفته‌اند در یک سلسله مراتب انباشته مرتب می‌شوند. هر مجموعه از این سلسله مراتب با یک عدد ترتیبی α مشخص می‌گردد (با استفاده از استقرای ترامتناهی)، که به عنوان مرتبه آن شناخته می‌شود. مرتبه یک مجموعه خالص X به عنوان کوچکترین کران بالای همه جانشین‌های مرتبه‌های اعضای X تعریف می‌شود. برای مثال، مجموعه تهی مرتبه ۰ خوانده می‌شود، درحالی که مجموعه که تنها شامل مجموعه تهی است مرتبه ۱ خوانده می‌شود. برای هر عدد ترتیبی α، مجموعه V_α به عنوان مجموعه‌ای تعریف می‌شود که شامل همه مجموعه‌های خالص با مرتبه کمتر از α است. کل جهان ون نویمان با V نشان داده می‌شود.

نظریه اصل موضوعی مجموعه‌ها

نظریه مقدماتی مجموعه‌ها می‌تواند به صورت غیررسمی و طبیعی مطالعه شود، که بتوان آن را در مدارس ابتدایی با استفاده از نمودار ون تدریس کرد. رویکرد طبیعی تلویحاً فرض می‌کند که یک مجموعه می‌تواند از تشکیل کلاس کل اشیایی تولید شود که از یک شرط خاص تبعیت می‌کنند. این فرض تناقض‌هایی را به دنبال دارد، که ساده‌ترین و معروف‌ترین آن‌ها پارادوکس راسل و پارادوکس بورالی-فورتی هستند. نظریه اصل موضوعی مجموعه‌ها در اصل درست شده بود که نظریه مجموعه‌ها را از چنین پارادوکس‌هایی برهاند. گسترده‌ترین سیستم مطالعه شده نظریه اصل موضوعی مجموعه‌ها اذعان می‌کند که همه مجموعه‌ها از یک سلسله مراتب انباشته می‌آیند. همچنین سیستم‌هایی در دو ذائقه می‌آیند، آن‌هایی که هستی‌شناسیشان از:

• تنها مجموعهها تشکیل می‌شود. این رایج‌ترین نظریه اصل موضوعی مجموعه‌ها، نظریه مجموعه‌های زرملو-فرانکل (ZFC) را شامل می‌شود، که خود شامل اصل انتخاب است. قطعه‌های ZFC شامل:
  • نظریه مجموعه‌های زرملو، که طرح اصل جایگزینی را با اصل موضوع جداسازی جایگزین می‌کند.
  • نظریه عمومی مجموعه‌ها، قطعه کوچکی از نظریه مجموهای زرملو که برای اصول پئانو و مجموعه‌های متناهی کافی است.
  • نظریه مجموعه‌های کریپکی-پلاتک، که اصول نامتناهی، مجموعه توانی و انتخاب را حذف می‌کند، و اصل موضوع جداسازی و جایگذاری را تضعیف می‌کند.
• «مجموعه‌ها و کلاس‌های مناسب» تشکیل می‌شود. این‌ها شامل نظریه مجموعه‌ها ی فون نویمان-برنایز-گودل، که برای نظریه‌های در مورد مجموعه‌های تنها به اندازه ZFC قدرتمند است، و همچنین نظریه مجموعه‌های مورس-کلی و نظریه مجموعه‌های تارسکی-گروتندیک، که هر دو از ZFC قوی ترند.

سیستم‌های بالا می‌توانند طوری اصلاح شوند که یورالمنت (به انگلیسی: urelement) یا عناصر اساسی، اشیایی که می‌توانند اعضای مجموعه‌ها باشند ولی خودشان مجموعه نیستند و عضوی ندارند، را مجاز بشمرند. سیستم‌های مبانی جدید NFU (شامل یورالمنت‌ها) و NF (فاقد آنها) بر پایه یک سلسله مراتب انباشته نیستند.NF و NFU شامل یک «مجموعه همه چیز» هستند، مرتبط با اینکه هر مجموعه یک متمم دارد. در این سیستم‌ها عناصر اساسی مهم هستند، چون NF، نه NFU، مجموعه‌هایی را تولید می‌کند که اصل موضوعه انتخاب آن‌ها را در برندارد. سیستم‌های نظریه مجموعه‌های ساختمانی، مانند CFT, CZF و IFZ، اصول مجموعه ایشان را در منطق شهودی به جای منطق مرتبه اول جای دهند. در حالی که سیستم‌های دیگر منطق استاندارد مرتبه اول را قبول می‌کنند اما یک رابطه عضویت غیر استاندارد را پوشش می‌دهند. این شامل نظریه ناهنجار مجموعه‌ها و نظریه فازی مجموعه‌ها می‌شود، که در آن‌ها ارزش فرمول اتمی که رابطه عضویت را دربردارد، به سادگی درست یا غلط نیست. مدل ارزش بولی ZFC یک موضوع مرتبط هستند. یک غنی‌سازی ZFC که نظریه درونی مجموعه‌ها نامیده می‌شود، توسط ادوارد نلسون در ۱۹۹۷ ارائه شد.

بنداشت نگره بنداشتی کوده‌ها (Axiomatic set theory)

بنداشت جداسازی

بنداشت جدایش یکی از بنداشت‌های نگره کوده‌ها است که می‌گوید اگر x یک کوده و A یک ویژگی رایه نخست باشد آنگاه گردایه اندام‌های x که ویژگی A را دارند خود یک کوده است.

کاربردها

بسیاری از مفاهیم ریاضی می‌توانند به صورت دقیق تنها با استفاده از مفاهیم نظری بیان شوند. برای مثال، ساختارهای متنوعی مانند گراف، خمینه‌ها، حلقه‌ها، و فضاهای برداری همه می‌توانند به صورتی تعریف شوند که خواص اصل موضوعی متنوعی را داشته باشند. رابطه هم‌ارزی و روابط ترتیب در ریاضیات همه جا هستند، و نظریه روابط ریاضی در نظریه مجموعه‌ها می‌توانند تعریف شوند. نظریه مجموعه‌ها همچنین یک سازمان نویدبخش برای بیشتر ریاضیات است. از زمان انتشار اولین جلد «مبادی ریاضیات» ادعا شده‌است که بیشتر یا حتی همه نظریه‌های ریاضی می‌توانند با استفاده از یک مجموعهٔ اصول موضوعه خوب طراحی شده برای نظریه مجموعه‌ها که به وسیله تعریف‌های زیادی بهبود یافته، با استفاده از منطق مرتبه اول یا منطق مرتبه دوم، مشتق شوند. برای مثال، خواص اعداد طبیعی و اعداد حقیقی از دل نظریه مجموعه‌ها نتیجه می‌شود، هر سیستم عددی را با یک کلاس هم‌ارزی تحت یک رابطه هم‌ارزی مناسب با زمینه یک مجموعه نامتناهی شناخت. نظریه مجموعه‌ها به عنوان یک نظام برای آنالیز ریاضی، توپولوژی، جبر مجرد و ریاضیات گسسته، مشابهاً بدون بحث است. ریاضی دانان می‌پذیرند که نظریه‌های این ناحیه می‌توانند از تعریف‌های مرتبط و اصول موضوعه نظریه مجموعه‌ها ناشی شوند. تعداد کمی از مشتقات کامل نظریه‌های پیچیده ریاضی از نظریه مجموعه‌ها رسماً تأیید شده‌اند، هرچند مشتقات رسمی اینچنین معمولاً از اثبات‌های زبان طبیعی که ریاضی‌دان‌ها معمولاً ارائه می‌دهند بسیار طولانی ترند. یک پروژه تأیید صحت متامث، شامل مشتقات بیش از ۱۰۰۰۰ نظریه از اصول موضوعه ZFC تا استفاده از منطق مرتبه اول می‌شود.

اصل موضوع گسترش

اصل موضوعی گسترش نخستین اصل موضوع نظریه اصل موضوعی مجموعه‌ها است و گویای این است که دو مجموعه x و y برابرند اگر و تنها اگر اعضای یکسانی داشته باشند.

نواحی مطالعه

نظریه مجموعه‌ها یک ناحیه وسیع تحقیق در ریاضیات، همراه با تعداد زیادی زیرموضوع مرتبط است.

منابع

https://en.wiki.x.io/wiki/Set_theory

برای مطالعهٔ بیشتر

• Devlin, Keith, 1993. The Joy of Sets (2nd ed.). Springer Verlag, ISBN 0-387-94094-4
• Ferreirós, Jose, 2007 (1999). Labyrinth of Thought: A history of set theory and its role in modern mathematics. Basel, Birkhäuser. ISBN 978-3-7643-8349-7
• Johnson, Philip, 1972. A History of Set Theory. Prindle, Weber & Schmidt ISBN 0-87150-154-6
• Kunen, Kenneth, 1980. Set Theory: An Introduction to Independence Proofs. North-Holland, ISBN 0-444-85401-0.
• Potter, Michael, 2004. Set Theory and Its Philosophy: A Critical Introduction. Oxford University Press.
• Tiles, Mary, 2004 (1989). The Philosophy of Set Theory: An Historical Introduction to Cantor's Paradise. Dover Publications. ISBN 978-0-486-43520-6