فضای برداری
در ریاضیات، فیزیک و مهندسی، فضای برداری (یا فضای خطی) (به انگلیسی: Vector Space) به مجموعهای از اشیاء بهنام بردار گفته میشود که روی آنها دو عمل «جمع» و «ضرب اسکالر در بردار» تعریف شدهباشد. این اسکالر معمولاً عددی حقیقی است، اما در حالت کلی میتوان آن را عضو هر میدانی مانند اعداد مختلط در نظر گرفت. این دو عمل باید طوری تعریف شده باشند که چند قاعده یا اصل موضوع را برآورند. برای مشخص کردن اینکه اسکالر ضرب نردهای، حقیقیست یا مختلط، از عبارتهای فضای برداری حقیقی یا فضای برداری مختلط استفاده میشود.[۱]

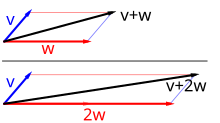
مجموعهٔ بردارهای اقلیدسی نمونه ای از فضای برداری است. از بردارهای اقلیدسی در نمایش کمیتهای برداری در فیزیک استفاده میشود. برای پیدا کردن نیروی خالص وارد بر یک جسم، همهٔ نیروهای وارد بر آن را جمع برداری میکنیم؛ همچنین، بردار نیرو از ضرب بردار شتاب در جرم (یک کمیت نردهای) بهدست میآید.
در حالت کلی، بردارهای یک فضای برداری لزوماً یک بردار اقلیدسی نیستند پس لزوماً با فلش نمایش داده نمیشوند. به عبارت دیگر، بردار یک چیز انتزاعی است و تنها گاهی میتوان آنها را با پیکان (فلش) نمایش داد.
فضاهای برداری در ریاضیات، علم و مهندسی، گسترده استفاده میشوند. در جبر خطی، از فضای برداری در کار با دستگاههای معادلات خطی استفاده میشوند. همچنین از فضاهای برداری برای حل معادلات دیفرانسیل با مشتقات جزئی و بسط فوریه استفاده میشود.
فضای برداری، سنگ بنایی برای تعمیم به چیزهای هندسی و فیزیکی کلیتر، مانند ماتریس و تنسورها هستند.
تعریف
ویرایشیک فضای برداری روی یک میدان اسکالر (مانند میدان اعداد حقیقی ) یک مجموعه از بردارها بههمراه دو عمل جمع و ضرب اسکالر است.
- مجموعهٔ ناتهی است.
- عمل جمع یک عمل دوتایی روی دو بردار از است.
- عمل ضرب یک عمل دوتایی بین یک بردار از و یک اسکالر از است. ضرب در اسکالر، نباید با ضرب داخلی اشتباه شود، در ضرب داخلی دو بردار در هم ضرب میشوند و یک اسکالر به دست میآید، درحالیکه در ضرب اسکالر، یک بردار در یک اسکالر ضرب میشود و یک بردار جدید به دست میآید.
اصول موضوعی
ویرایشبه ازای هر بردار و و از مجموعهٔ و هر اسکالر و از میدان باید ده اصل موضوعی زیر رعایت شوند تا بتوان آنها را فضای برداری تعریف کرد:[۲]
| قاعده | توضیح | دقیق | ||
|---|---|---|---|---|
| بیان جبر مجرد | بیان ساده | |||
| بستار | بسته نسبت به جمع | جمع و در وجود داشته باشد. | ||
| بسته نسبت به ضرب | ضرب و در وجود داشته باشد. | |||
| نسبت به + گروه آبلی باشد | گروه باشد | همانی در جمع | یک عنصر همانی در وجود دارد که جمع آن با هر برداری همان بردار شود. | |
| وارون در جمع | یک عنصر وارون در وجود دارد که جمعش با برابر عنصر همانی شود. | |||
| شرکتپذیری در جمع | پرانتزگذاری در جمع بیتأثیر باشد. | |||
| جابهجاپذیری در جمع | جابهجایی در جمع بیتأثیر باشد. | |||
| این گروه یک -مدول باشد | همانی ضرب | ضرب عنصر همانی میدان در هر برداری همان بردار شود. | ||
| توزیعپذیری ضرب | پخشپذیری اسکالر | ضرب اسکالرها در جمع بردارها پخشپذیر باشد. | ||
| پخشپذیری بردار | ضرب بردارها در جمع اسکالرها پخشپذیر باشد. | |||
| سازگاری ضرب میدان با ضرب فضای برداری | پرانتزگذاری ضرب اسکالرها و ضرب بردار در اسکالر بیتأثیر باشد. | |||
جمع و ضرب عملگر هستند و طبق تعریف عملگر، بسته بودن جزو قواعد آنها هست. در نتیجه دو قاعدهٔ ابتدایی در مورد بسته بودن تکراری است و در کتابهای منبع جدیدتر نوشته نمیشوند.
نتایج
ویرایشاز اصول یادشده میتوان به نتایج زیر رسید:[۱]
- عنصر همانی یکتا است.
- وارون جمع هر برداری یکتا است.
پوچساز
ویرایشهرگاه فضایی برداری باشد بر میدان و زیرمجموعهای از باشد، در این صورت پوچساز عبارتست از تابعکهای خطی روی که به ازای هر در داریم . پوچساز را با نشان میدهند.
در واقع داریم:
جستارهای وابسته
ویرایش- زیرفضای خطی
- استقلال خطی
- پوشش خطی (اسپن)
- پایه (جبر خطی)
- بعد (فضای برداری)
- تحلیل مولفههای اصلی
- میدان برداری
- نرمها
فضاهای برداری با ساختار بیشتر
ویرایشمنابع
ویرایش- جبر خطّی عددی (انگلیسی)
- مقدمهای بر ریاضیات کاربردی (انگلیسی)
- فضای برداری
- Strang, Gilbert (۱۹ ژوئیه ۲۰۰۵), Linear Algebra and Its Applications (4th ed.), Brooks Cole, ISBN 978-0-03-010567-8
- Kenneth Hoffman, Ray Kunze، «۲»، Linear Algebra (ویراست Second Edition)، Prentice-Hall, Inc.، ص. ۲۸


