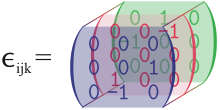
نماد لوی-چیویتا در سه بعد به صورت زیر تعریف می‌شود:
ε
i
j
k
=
{
+
1
if
(
i
,
j
,
k
)
is
(
1
,
2
,
3
)
,
(
3
,
1
,
2
)
or
(
2
,
3
,
1
)
,
−
1
if
(
i
,
j
,
k
)
is
(
3
,
2
,
1
)
,
(
1
,
3
,
2
)
or
(
2
,
1
,
3
)
,
0
otherwise:
i
=
j
or
j
=
k
or
k
=
i
,
{\displaystyle \varepsilon _{ijk}={\begin{cases}+1&{\mbox{if }}(i,j,k){\mbox{ is }}(1,2,3),(3,1,2){\mbox{ or }}(2,3,1),\\-1&{\mbox{if }}(i,j,k){\mbox{ is }}(3,2,1),(1,3,2){\mbox{ or }}(2,1,3),\\0&{\mbox{otherwise: }}i=j{\mbox{ or }}j=k{\mbox{ or }}k=i,\end{cases}}}
همچنین این نماد را می‌توان از رابطه زیر بدست آورد:
ε
i
j
k
=
−
[
(
i
−
j
)
2
%
3
]
[
(
i
−
k
)
2
%
3
]
[
(
j
−
k
)
2
%
3
]
[
(
j
−
(
i
%
3
)
−
1
2
)
2
−
5
4
]
{\displaystyle \varepsilon _{ijk}=-[(i-j)^{2}\%3][(i-k)^{2}\%3][(j-k)^{2}\%3][(j-(i\%3)-{\frac {1}{2}})^{2}-{\frac {5}{4}}]}
که % نماد عملگر باقی‌مانده است.
از این نماد مفید برای ساده‌سازی عبارات طولانی و پیچیده استفاده می‌شود. به عنوان مثال در ضرب خارجی a و b داریم:
a
×
b
=
|
e
1
e
2
e
3
a
1
a
2
a
3
b
1
b
2
b
3
|
=
∑
i
,
j
,
k
=
1
3
ε
i
j
k
e
i
a
j
b
k
{\displaystyle \mathbf {a\times b} ={\begin{vmatrix}\mathbf {e_{1}} &\mathbf {e_{2}} &\mathbf {e_{3}} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}=\sum _{i,j,k=1}^{3}\varepsilon _{ijk}\mathbf {e_{i}} a_{j}b_{k}}
که با استفاده از قرارداد جمع‌زنی انیشتین به صورت زیر در می‌آید:
a
×
b
=
ε
i
j
k
e
i
a
j
b
k
{\displaystyle \mathbf {a\times b} =\varepsilon _{ijk}\mathbf {e_{i}} a_{j}b_{k}}
و یا اگر A یک ماتریس ۳در۳ باشد، دترمینان آن را به صورت خلاصه زیر می‌توان نمایش داد:
det
A
=
∑
i
,
j
,
k
=
1
3
ε
i
j
k
a
1
i
a
2
j
a
3
k
=
ε
i
j
k
a
1
i
a
2
j
a
3
k
{\displaystyle \det A=\sum _{i,j,k=1}^{3}\varepsilon _{ijk}a_{1i}a_{2j}a_{3k}=\varepsilon _{ijk}a_{1i}a_{2j}a_{3k}}
این نماد را برای ابعاد دیگر هم می‌توان تعریف کرد. به این صورت که برای
ε
i
j
k
l
{\displaystyle \varepsilon _{ijkl}}
i
j
k
l
.
.
.
{\displaystyle ijkl...}
(
1
,
2
,
3
,
4
,
.
.
.
)
{\displaystyle (1,2,3,4,...)}
+
1
{\displaystyle +1}
−
1
{\displaystyle -1}
ε
i
j
k
ℓ
…
=
{
+
1
if
(
i
,
j
,
k
,
ℓ
,
…
)
is an even permutation of
(
1
,
2
,
3
,
4
,
…
)
−
1
if
(
i
,
j
,
k
,
ℓ
,
…
)
is an odd permutation of
(
1
,
2
,
3
,
4
,
…
)
0
if any two labels are the same
{\displaystyle \varepsilon _{ijk\ell \dots }=\left\{{\begin{matrix}+1&{\mbox{if }}(i,j,k,\ell ,\dots ){\mbox{ is an even permutation of }}(1,2,3,4,\dots )\\-1&{\mbox{if }}(i,j,k,\ell ,\dots ){\mbox{ is an odd permutation of }}(1,2,3,4,\dots )\\0&{\mbox{if any two labels are the same}}\end{matrix}}\right.}
![{\displaystyle \varepsilon _{ijk}=-[(i-j)^{2}\%3][(i-k)^{2}\%3][(j-k)^{2}\%3][(j-(i\%3)-{\frac {1}{2}})^{2}-{\frac {5}{4}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fab4f9687fdd29f3e059460b812154f9654e49f7)
