برای بردارهای یکّهٔ پایه تساویهای زیر برقرار اند[ ۲] [ ۳]
روشی برای حفظ کردن ضرب خارجی
i
^
{\displaystyle {\hat {i}}}
j
^
{\displaystyle {\hat {j}}}
k
^
{\displaystyle {\hat {k}}}
i
^
×
j
^
=
−
j
^
×
i
^
=
k
^
{\displaystyle {\hat {i}}\times {\hat {j}}=-{\hat {j}}\times {\hat {i}}={\hat {k}}}
j
^
×
k
^
=
−
k
^
×
j
^
=
i
^
{\displaystyle {\hat {j}}\times {\hat {k}}=-{\hat {k}}\times {\hat {j}}={\hat {i}}}
k
^
×
i
^
=
−
i
^
×
k
^
=
j
^
{\displaystyle {\hat {k}}\times {\hat {i}}=-{\hat {i}}\times {\hat {k}}={\hat {j}}}
i
^
×
i
^
=
0
→
j
^
×
j
^
=
0
→
k
^
×
k
^
=
0
→
{\displaystyle {\hat {i}}\times {\hat {i}}={\vec {0}}\qquad {\hat {j}}\times {\hat {j}}={\vec {0}}\qquad {\hat {k}}\times {\hat {k}}={\vec {0}}}
از تساویهای فوق میتوان فرمول ضرب خارجی را نتیجه گرفت[ ۲]
اگر
a
→
=
(
a
x
,
a
y
,
a
z
)
{\displaystyle {\vec {a}}=(a_{x},a_{y},a_{z})}
b
→
=
(
b
x
,
b
y
,
b
z
)
{\displaystyle {\vec {b}}=(b_{x},b_{y},b_{z})}
a
→
×
b
→
=
(
a
y
b
z
−
a
z
b
y
,
a
z
b
x
−
a
x
b
z
,
a
x
b
y
−
a
y
b
x
)
{\displaystyle {\vec {a}}\times {\vec {b}}=(a_{y}b_{z}-a_{z}b_{y},a_{z}b_{x}-a_{x}b_{z},a_{x}b_{y}-a_{y}b_{x})}
برای حفظکردن راحتتر ضرب خارجی میتوان از تساوی زیر کمک گرفت[ ۲] [ ۳]
a
→
×
b
→
=
|
i
^
j
^
k
^
a
x
a
y
a
z
b
x
b
y
b
z
|
{\displaystyle {\vec {a}}\times {\vec {b}}={\begin{vmatrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\\\end{vmatrix}}}
این دترمینان را میتوان با روش ساروس محاسبه کرد که در نهایت به فرمول بیان ریاضی میرسد.
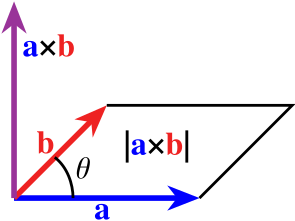
قانون دست راست جهت بردارِ حاصل از ضرب خارجی، عمود بر هر دو بردار
a
→
{\displaystyle {\vec {a}}}
b
→
{\displaystyle {\vec {b}}}
قانون دست راست قابل تشخیص است و طول آن برابر مساحت متوازیالاضلاعی با اضلاع بردارهای اوّلیّه است[ ۴]
θ
{\displaystyle \theta }
[ ۲]
|
a
→
×
b
→
|
=
|
a
→
|
|
b
→
|
sin
θ
{\displaystyle \left\vert {\vec {a}}\times {\vec {b}}\right\vert =\left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert \sin \theta }
اگر بردارها همراستا باشند یا یکی از بردارها صفر باشد، حاصل ضرب خارجی صفر خواهد شد.
جابهجایی ندارد ولی[ ۲]
a
→
×
b
→
=
−
b
→
×
a
→
{\displaystyle {\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}}
پخشپذیری [ ۲]
a
→
×
(
b
→
+
c
→
)
=
a
→
×
b
→
+
a
→
×
c
→
{\displaystyle {\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}}
شرکتپذیری ندارد ولی از تساوی جاکوبی پیروی میکند:
a
→
×
(
b
→
×
c
→
)
+
b
→
×
(
c
→
×
a
→
)
+
c
→
×
(
a
→
×
b
→
)
=
0
→
{\displaystyle {\vec {a}}\times ({\vec {b}}\times {\vec {c}})+{\vec {b}}\times ({\vec {c}}\times {\vec {a}})+{\vec {c}}\times ({\vec {a}}\times {\vec {b}})={\vec {0}}}
ضرب در عدد[ ۲]
(
r
a
→
)
×
b
→
=
a
→
×
(
r
b
→
)
=
r
(
a
→
×
b
→
)
{\displaystyle (r{\vec {a}})\times {\vec {b}}={\vec {a}}\times (r{\vec {b}})=r({\vec {a}}\times {\vec {b}})}
a
→
×
a
→
=
0
→
{\displaystyle {\vec {a}}\times {\vec {a}}={\vec {0}}}
a
→
×
b
→
=
0
→
⟺
a
→
∥
b
→
{\displaystyle {\vec {a}}\times {\vec {b}}={\vec {0}}\Longleftrightarrow {\vec {a}}\parallel {\vec {b}}}
[ ۲]
به کمک اتّحاد لاگرانژ میتوان دریافت[ ۵]
|
a
→
×
b
→
|
2
=
|
a
→
|
2
|
b
→
|
2
−
(
a
→
⋅
b
→
)
2
{\displaystyle \left\vert {\vec {a}}\times {\vec {b}}\right\vert ^{2}=\left\vert {\vec {a}}\right\vert ^{2}\left\vert {\vec {b}}\right\vert ^{2}-({\vec {a}}\cdot {\vec {b}})^{2}}