میدان مغناطیسی

در الکترومغناطیس کلاسیک، میدان مغناطیسی یک میدان برداری است که تأثیر مغناطیسی بر بارهای الکتریکی متحرک، جریان‌های الکتریکی و مواد مغناطیسی را توصیف می‌کند. برای نمونه، بر یک بار الکتریکی متحرک در میدان مغناطیسی، نیرویی عمود بر سرعت و میدان مغناطیسی، وارد می‌شود.

میدان مغناطیسی آهن‌ربای دائمی، مواد فِرّومغناطیسی مانند آهن را می‌کِشد و آهن‌رباهای دیگر را کشیده یا می‌رانَد. افزون‌براین، یک میدان مغناطیسی متغیر با مکان، با تأثیر بر حرکت الکترون‌های اتمی بیرونی، بر برخی از مواد غیرمغناطیسی نیرو وارد می‌کند.

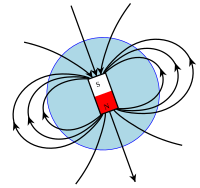
میدان‌های مغناطیسی، اطراف مواد مغناطیسی هستند و از سوی جریان‌های الکتریکی، مانند جریان الکتریکی سیم‌پیچ‌ها، یا میدان‌های الکتریکی متغیر با زمان پدید می‌آیند. از آنجاکه میدان مغناطیسی، شدت و جهت دارد، با بردار توصیف می‌شود. میدان‌ مغناطیسی با حرکت بارهای الکتریکی و گشتاورهای مغناطیسی ذاتی ذرات بنیادی، یعنی اسپین آنها، تولید می‌شود. نیروی مغناطیسی، یکی از چهار نیروی اساسی طبیعت است.

از میدان‌های مغناطیسی در سراسر تکنولوژی مدرن، به‌ویژه در مهندسی برق و الکترومکانیک استفاده می‌شود، مانند میدان‌های مغناطیسی چرخنده در موتورهای الکتریکی و ژنراتورها. زمین هم میدان مغناطیسی دارد، که از لایه اوزون زمین در برابر باد خورشیدی محافظت می‌کند و در جهت‌یابی با قطب‌نما مهم است.

شدت میدان و چگالی شار مغناطیسی

در توصیف میدان مغناطیسی، از دو میدان برداری استفاده می‌شود، که شدت میدان (H) و چگالی شار میدان (B) نام دارند.

Alternative names for B
name	used by
magnetic flux density	electrical engineers
magnetic induction	applied mathematicians electronics engineers
magnetic field	physicists

Alternative names for H
name	used by
magnetic field intensity	electrical engineers
magnetic field strength	electronics engineers
auxiliary magnetic field	applied mathematicians
magnetizing field	physicists

بیرون مواد، میدان‌های B و H، کم‌وبیش یکی هستند. این دو تنها در واحد و مقدار متفاوتند و در تغییرات زمانی و مکانی تفاوتی ندارند. B به جریان بستگی دارد، چه ماکروسکوپی و چه میکروسکوپی، مانند حرکت الکترون به دور هسته. در حالی که H به جریان‌های ماکروسکوپی و برداری که به شار مغناطیسی بسیار نزدیک است، بستگی دارد.

B را می‌توان بر اساس اثرات آن روی محیط نیز تعریف کرد. برای مثال، حرکت یک ذره با بار الکتریکی q و با سرعت v در میدان B، نیرویی را تعریف می‌کند که نیروی لورنتس نامیده می‌شود. در سیستم SI، نیروی لورنتس برابر است با:

$\mathbf {F} =q\left(\mathbf {v} \times \mathbf {B} \right)$

که در آن ×، ضرب خارجی بردارهاست.

برای دوقطبی مغناطیسی لحظه‌ای m (آمپر متر مربع)، B را می‌توان به‌گونه‌ای دیگر و بر اساس گشتاور دوقطبی مغناطیسی در میدان B تعریف کرد:

{\boldsymbol {\tau }}=\mathbf {m_{m}} \times \mathbf {B}

واحد B در سیستم SI، تسلا و در سیستم cgs، گاوس است. (۱ تسلا = ۱۰۰۰۰ گاوس). با در نظر گرفتن رابطه نیروی لورنتس،

$\mathbf {F} =q\,\mathbf {v} \times \mathbf {B}$

تسلا برابر با (کولن متر) / (نیوتن ثانیه) خواهد شد.

H به عنوان اصلاحی برای B با لحاظ کردن اثر میدان مغناطیسی تولیدشده درون مواد خواهد بود، به‌طوری‌که (در SI):

\mathbf {H} \ \equiv \ {\frac {\mathbf {B} }{\mu _{0}}}-\mathbf {M} ,

که M، مغناطش ماده و μ₀ نفوذپذیری (تراوایی) مغناطیسی در فضای آزاد است.^[۱] یکای H در سیستم SI، آمپر بر متر و در سیستم cgs، اُرستِد است.

در موادی که M متناسب با B است، رابطه B و H را می‌توان ساده‌تر نوشت:

H = B/μ

که در آن μ پارامتر وابسته به ماده است و نفوذپذیری نام دارد. در فضای آزاد، هیچ مغناطشی وجود ندارد، بنابراین

H = B/μ

برای بسیاری از مواد، B و M رابطه ساده‌ای ندارند. برای مثال، مواد فِرّومغناطیسی و ابررساناها خاصیت مغناطشی دارند که تابعی چندمتغیره از B و مربوط به پسماند مغناطیسی است.

نیروی الکترومغناطیسی وارد بر سیم جریان‌دار

اگر سیمی جریان‌دار در یک میدان مغناطیسی قرار گیرد نیرویی بر آن وارد می‌شود. این نیرو با طول سیم (L) و چگالی شار مغناطیسی (B) رابطه مستقیم دارد؛ $F=L\,I\,B\,\sin \alpha$ .

بنابراین رابطه، اگر سیم با میدان مغناطیسی هم‌راستا باشد، نیروی وارد بر آن صفر است زیرا α=۰° Sin 0°=۰ یا α=۱۸۰° Sin 180°=۰ در نتیجه ۰=F است. اگر سیم، عمود بر میدان باشد، نیروی وارد بر آن بیشترین است. اگر سیم اریب بر میدان باشد، کافی‌ست راستای آن را به دو مؤلفه عمود بر میدان و هم‌راستا با آن تقسیم کرده و تنها مؤلفه عمود را در نظر گرفت. برای پیدا کردن جهت میدان، بر اساس قاعده دست راست عمل می‌شود.

میدان مغناطیسی اطراف سیم

اگر از سیمی، جریان بگذرد، اطراف آن سیم، میدان مغناطیسی پدید می‌آید.

میدان مغناطیسی داخل سیم‌لوله

میدان مغناطیسی B داخل یک سیم‌لوله‌ بی‌هسته، به تعداد دور سیم در واحد متر، جریان سیم و ثابت تراوایی مغناطیسی فضای آزاد بستگی دارد.

$B=\mu _{0}NI/L=\mu _{0}nI$

که در آن، $\mu _{0}=4\pi \times 10^{-4}\;T\,m/A$ تراوایی مغناطیسی فضای آزاد، $N$ تعداد دور حلقه، $I$ جریان بر حسب آمپر، $L$ طول سیم‌لوله بر حسب متر، و $n$ تعداد حلقه‌ها در واحد طول است.

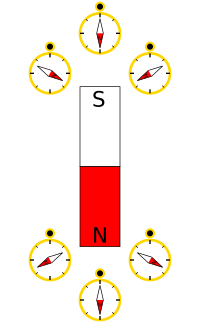
میدان مغناطیسی و آهن‌ربای دائم

آهن‌ربای دائم، مداوم میدان‌ مغناطیسی تولید می‌کند. آهن‌ربا، دو قطب شمال و جنوب دارد و از مواد فِرّومغناطیسی مانند آهن و نیکل که مغناطیسی شده‌اند ساخته‌شده‌اند.

شعاع‌های الکترون در یک دایره حرکت می‌کنند. نور نتیجه برانگیختگی اتم‌های گاز در لامپ است

مفهوم قطب‌های مغناطیسی، آن‌چه درون آهن‌ربا میگذرد را به‌درستی بیان نمی‌کند (نگاه کنید به فِرّومغناطیس شدن). شار مغناطیسی وجود ندارد. برای مثال، بر خلاف شار الکتریکی، یک آهن‌ربا نمی‌تواند قطب‌ جداگانه‌ای در یک سمت (شمال) و قطب دیگری در سمت دیگر (جنوب) داشته باشد؛ همه آهنرباها یک جفت قطب شمال و جنوب دارند. افزون‌براین، یک آهنربای کوچک که درون یک آهنربای بزرگتر قرار گرفته، در جهتی مخالف آنچه از میدان H انتظار می‌رود قرار می‌گیرد.

مغناطیسی شدن، با حلقه‌های اتمی جریان که در سراسر آهن‌ربا توزیع شده‌اند، صحیح‌تر توصیف می‌شود.^[۲] در این توصیف، یک آهنربا، از بسیاری آهنرباهای کوچک، به نام دوقطبی مغناطیسی که هر کدام یک جفت قطب شمال و جنوب مربوط به جریان الکتریکی دارند، تشکیل شده‌است. هنگامی که در ترکیب آن‌ها به صورت یک آهنربا که قدرت مغناطیسی دارد m. که برای راحتی محاسبات ریاضی است، همچنین با توجه به جهت متناظر با جهت‌گیری‌های میدان مغناطیسی آن را تعریف می‌کنند. برای آهنرباهای ساده، m در جهت خط از جنوب تا قطب شمال آهن‌ربا کشیده شده‌است. نیروی جاذبه میان دو آهنربا، پیچیده و وابسته به قدرت، جهت‌ و فاصله آن دو است. نیروی مغناطیسی هر آهنربا بستگی به آهنربا و میدان مغناطیسی B^[۳] دارد. میدان B یک آهنربا ی کوچک پیچیده‌تر است. نیرو یک آهنربا با مغناطیسی‌شدگی m، در اثر میدان مغناطیسی B برابر است با:^[۴]

\mathbf {F} =\mathbf {\nabla } \left(\mathbf {m} \cdot \mathbf {B} \right),

که در آن∇ گرادیان است. در هر واحد از فاصله و جهت است که افزایش حداکثر m.B را محصول است (نقطه معادله زیر را ایجاد می‌کند. ضرب داخلی:(m · B = mBcos(θکه در آن m و B نشان از اندازه بردارهای m و B است و θ زاویه بین آن‌ها است) این معادله صرفاً فقط برای آهنرباهای صفر اندازه معتبر است، اما اغلب می‌توان به عنوان تقریبی برای آهن‌رباهای نه چندان بزرگ استفاده کرد. نیروی مغناطیسی در آهنرباهای بزرگتر از تقسیم آن‌ها به مناطق کوچکتر با m مشخص و سپس جمعبندی نیروهای در هر یک از این مناطق تعیین می‌شود.

گشتاور نیروی آهن‌ربا در میدان B

طرحی از آهن‌ربای چهار قطبی. چهار نوک ثابت قطب‌های آهنربا هستند که دو تای آن‌ها با قطب N و دو تا با قطب S مخالفت می‌کنند

گشتاور نیروی یک آهن‌ربا که در میدان مغناطیسی خارجی قرار گرفته را می‌توان با قرار دادن دو آهنربا در نزدیکی هم درحالی‌که یکی از آن‌ها شروع به چرخش می‌کنند دید. گشتاور نیروی مغناطیسی برای موتورهای الکتریکی ضروری است. در یک موتور ساده، آهنربا روی یک محور که آزادانه می‌چرخد قرار گرفته‌است و در میدان مغناطیسی ردیفی از الکترومغناطیسی‌ها قرار دارد.. با سوئیچینگ مداوم جریان الکتریکی از هر کدام از آهنرباهای الکتریکی، با توجه به تغییر میدان مغناطیسی آن‌ها، مانند قطب شمال و جنوب کنار روتور، گشتاور حاصل به محور منتقل می‌شود. میدان مغناطیسی دوار را مشاهده کنید. گشتاور مغناطیسی τ تمایل دارد قطب مغناطیسی با خطوط میدان B در یک امتداد قرار دهد (تا زمانی که m در جهت قطب‌های مغناطیسی است می‌توان گفت m تمایل دارد با B در یک امتداد قرار بگیرد) به همین دلیل است سوزن مغناطیسی قطب‌نما به سمت قطب شمال زمین منحرف می‌شود. با این تعریف، جهت میدان محلی مغناطیسی زمین جهتی است که در آن قطب شمال قطب‌نما (یا هر آهنربایی) تمایل به آن نقطه دارد. به‌طور ریاضی وار، گشتاور τ آهنربای کوچک متناسب با هر دوی میدان B اعمال شده مغناطیسی شدن آهنربا m می‌باشد:

{\boldsymbol {\tau }}=\mathbf {m} \times \mathbf {B} ,\,

که در آن × نشان دهندهٔ بردار ضرب خارجی است. در نظر داشته باشید که این معادله شامل تمام اطلاعات کیفی شامل بالا می‌باشد. هیچ گشتاور مغناطیسی در صورتی که m در امتداد B قرار بگیرد، وجود ندارد (مفهوم ضرب خارجی) علاوه بر این، در تمامی جهت‌ها گشتاوری که آن‌ها را به جهت B متمایل می‌کند احساس می‌شود.

کاربرد در پژوهش‌ها

در ژانویه ۲۰۱۳ فیزیک‌دانان ذرات یک گاز کوانتومی بر پایه پتاسیم ساختند. این گاز هنگامی که تحت تأثیر لیزر و میدان مغناطیسی قرار می‌گیرد به دماهای منفی می‌رسد. در این دمای ترمودینامیکی، ماده شروع به بروز دادن خواص ناشناخته می‌کند.^[۵]^[۶]

جستارهای وابسته

منابع

مبانی نظریه الکترومغناطیس، ریتس و میلفورد

آشنایی با حساب تنسوری و نسبیت، درک لاودن

↑ Durney, Carl H. and Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw Hill Financial. ISBN 0-07-018388-0.{{cite book}}: نگهداری یادکرد:نام‌های متعدد:فهرست نویسندگان (link)
↑ Jackson, John D. (1999). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. OCLC 224523909.
↑ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X. OCLC 40251748.
↑ Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8. OCLC 51095685.
↑ "Quantum gas temperature drops below absolute zero". Wired. 4 January 2013. Archived from the original on 24 January 2013. Retrieved 5 February 2013.
↑ "Quantum gas goes below absolute zero". Nature. 3 January 2013. Retrieved 5 February 2013.

Furlani, Edward P. (2001). Permanent Magnet and Electromechanical Devices: Materials, Analysis and Applications. Academic Press Series in Electromagnetism. ISBN 0-12-269951-3. OCLC 162129430.

[Durney,_Carl_H._and_Johnson,_Curtis_C._1969-1] Durney, Carl H. and Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw Hill Financial. ISBN 0-07-018388-0.{{cite book}}: نگهداری یادکرد:نام‌های متعدد:فهرست نویسندگان (link)

[2] Jackson, John D. (1999). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. OCLC 224523909.

[Griffiths,_David_J._1999-3] Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X. OCLC 40251748.

[4] Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8. OCLC 51095685.

[5] "Quantum gas temperature drops below absolute zero". Wired. 4 January 2013. Archived from the original on 24 January 2013. Retrieved 5 February 2013.

[6] "Quantum gas goes below absolute zero". Nature. 3 January 2013. Retrieved 5 February 2013.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]