مد نرمال

مُد نرمال یک سیستم دینامیکی، الگویی از حرکت است که در آن تمام قسمت‌های سیستم به صورت سینوسی با فرکانس یکسان و با یک فاز ثابت حرکت می‌کنند. این حرکت آزاد توصیف شده به عنوان مد نرمال ، در فرکانس‌های ثابت انجام می‌شود. فرکانس‌ها ی ثابت از مدهای نرمال یک سیستم به فرکانس‌های طبیعی یا فرکانس‌های تشدید معروف هستند. به عنوان مثال اجسامی مانند ساختمان، پل یا مولکول، دارای مجموعه ای از مدهای نرمال و فرکانس‌های طبیعی مربوط به آنهاست که به ساختار، مواد و شرایط مرزی آن اجسام بستگی دارد.

کلی‌ترین حرکت یک سیستم خطی، حاصل برهم نهی مدهای نرمال آن سیستم است. مدها به این معنا نرمال هستند که می‌توانند به‌طور مستقل حرکت کنند، به این معنی که تحریک یک مد هرگز باعث حرکت یک مد دیگر نمی‌شود. از نظر ریاضی، حالت مدهای نرمال با یکدیگر متعامد هستند.

یک دیسک دایره ای در حال ارتعاش در مد نرمال با شرایط مرزی پین شده در امتداد کل لبه بیرونی. حالت‌های دیگر را ببینید .

یک عکس لحظه ای از یک فنجان قهوه در حال لرزش در مد نرمال

تحریک مدهای نرمال یک قطره آب در هنگام اثر لیدنفراست

تعاریف کلی

مد (حالت)

در تئوری موج فیزیک و مهندسی، مد یک سیستم دینامیکی، حالت موج ایستاده برانگیخته ای است که در آن تمام اجزای سیستم به صورت سینوسی تحت تأثیر فرکانس ثابت مرتبط با آن مد تحت تأثیر قرار می‌گیرند.

مفهوم مُد به عنوان یک توصیف کلی از حالت‌های خاص یک نوسان در نظر گرفته می‌شود، زیرا هیچ سیستم واقعی نمی‌تواند به‌طور کامل تحت چارچوب موج ایستاده قرار گیرد؛ بنابراین سیستم دینامیکی را به صورت خطی در نظر می‌گیریم که در آن می‌توانیم حالت‌های سیستم را به صورت خطی برهم نهی کنیم.

مثال‌های معمول:

• در یک سیستم دینامیکی مکانیکی، یک طناب ارتعاشی واضح‌ترین مثال از یک مد است که در آن طناب یک محیط است، تنش روی طناب تحریک است و نسبت جابه جایی طناب به حالت استاتیک آن حالت یم متغیر مُدال می‌باشد.
• در یک سیستم دینامیکی آکوستیک، یک گام صدای واحد، یک مد است که در آن هوا، محیط، فشار صوتی در هوا تحریک و جابجایی مولکول‌های هوا متغیر مُدال است.
• در یک سیستم دینامیک سازه، یک ساختمان مرتفع که تحت بیشترین محور خمشی خود در نوسان است، یک مد است، که در آن تمام مصالح ساختمان - تحت ساده‌سازی عددی مناسب - محیط است، لرزه/باد/ استفاده‌های محیطی تحریک، و جابجایی‌ها متغیر مُدال هستند.
• در ارتباط با موسیقی، مدهای نرمال یک آلت موسیقی در حال ارتعاش overtones نامیده می‌شوند.
• در یک سیستم دینامیکی الکتریکی، یک حفره رزونانس ساخته شده از دیواره‌های فلزی نازک، که درون آن یک فضای خالی است، برای یک شتاب‌دهنده ذرات، یک سیستم موج ایستاده خالص است و بنابراین نمونه ای از حالتی است که در آن فضای توخالی حفره محیط (واسطه) است. منبع RF (کلایسترون یا یک منبع RF دیگر) تحریک و میدان الکترومغناطیسی متغیر مدال است.
• مفهوم مدهای نرمال در سیستم‌های دینامیکی دیگر مانند اپتیک، مکانیک کوانتومی، دینامیک اتمسفر و دینامیک مولکولی نیز کاربرد دارد.

اکثر سیستم‌های دینامیکی را می‌توان در چندین مد، احتمالاً به‌طور همزمان، برانگیخت. هر مد با توجه به فیلد متغیر مُدال، با یک یا چند فرکانس مشخص می‌شود. به عنوان مثال، یک طناب در حال ارتعاش در فضای دو بعدی به عنوان فرکانس تک شناخته می‌شود، اما در فضای سه بعدی به عنوان دو فرکانسی شناخته می‌شود.

در یک دامنه معین بر روی متغیر مدال، هر مد به دلیل تحریک سینوسی مقدار خاصی از انرژی را ذخیره می‌کند.

مد نرمال یا غالب یک سیستم با مدهای متعدد، مدی است که حداقل مقدار انرژی را برای دامنه معینی از متغیر مُدال ذخیره می‌کند، یا به‌طور معادل، برای مقدار ذخیره شده معینی از انرژی، مد غالب، مدی است که دامنه حداکثر متغیر مُدال را مشخص می‌کند.

عدد مد (mode number)

مد یک ارتعاش با فرکانس مودال و شکل مد (Mode shape) مشخص می‌شود و با توجه به تعداد نیم موج‌ها در ارتعاش شماره گذاری می‌شود. به عنوان مثال، اگر یک تیر در حال ارتعاش با دو سر گیردار، شکل مد نیمی از موج سینوسی (یک قله در تیر ارتعاشی) را نشان دهد، در مد ۱ (اول) می‌لرزد. اگر موج سینوسی کامل داشت (یک قله و یک فرورفتگی) در مد ۲ (دوم) می‌لرزد.

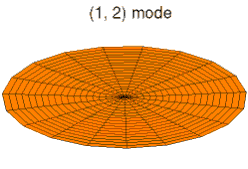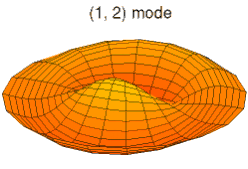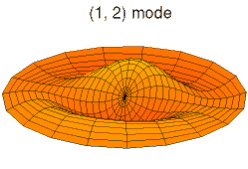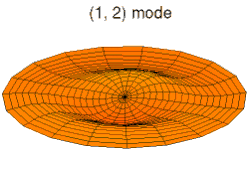
در یک سیستم با دو بُعد یا بیشتر، مانند دیسکی که در تصویر می‌بینید، هر مد با یک شماره مد تعریف می‌شود. با استفاده از مختصات قطبی، یک مختصات شعاعی و یک مختصات زاویه ای را در اختیار داریم. اگر از نقطه مرکز به سمت بیرون در امتداد مختصات شعاعی حرکت و اندازه‌گیری کنیم، با یک موج کامل مواجه می‌شویم، بنابراین عدد مد در جهت شعاعی ۲ است. به دلیل ماهیت ضد متقارن (که به آن تقارن کجی نیز گفته می‌شود) ارتعاش دیسک، جهت دیگر دشوارتر است زیرا فقط نیمی از دیسک در جهت زاویه ای در نظر گرفته می‌شود؛ بنابراین، با یک اندازه‌گیری ۱۸۰ درجه ای در امتداد جهت زاویه ای، با یک نیم موج مواجه می‌شوید، بنابراین عدد مد در جهت زاویه ای ۱ است. پس عدد مد سیستم ۲–۱ یا ۱–۲ است، این نوع شماره گذاری به ترتیب در نظر گرفتن مختصات بستگی دارد.

در سیستم‌های خطی هر مد کاملاً مستقل از سایر مدها است. به‌طور کلی همه مدها دارای فرکانس‌های متفاوت (مدهای پایین‌تر دارای فرکانس‌های پایین‌تر) و شکل مدهای متفاوت هستند.

گره‌ها

شکل مد یک درام، با خطوط گره ای که به رنگ سبز نشان داده شده است.

در یک سیستم تک بعدی در یک مد معین، ارتعاش دارای گره‌ها یا مکان‌هایی است که مقدار جابجایی در این مکان‌ها همیشه صفر است. این گره‌ها نمایانگر نقاطی در شکل مد هستند که شکل مد در آن‌ها صفر است. از آنجایی که ارتعاش یک سیستم به وسیله حاصل ضرب شکل مد در یک تابع از زمان به دست می‌آید، پس می‌توان نتیجه گرفت که جابجایی در نقاط گره همیشه صفر باقی می‌ماند.

یک سیستم دو بعدی را در نظر بگیرید، در این سیستم این گره‌ها تبدیل به خطوطی می‌شوند که مقدار جابجایی آنها همیشه صفر است. اگر تصویر بالا را تماشا کنید، دو دایره (یکی از آن‌ها در نیمه بین لبه و مرکز، و دیگری در خود لبه) و یک خط مستقیم که دیسک را در جایی که جابجایی نزدیک به صفر است به دو نیم تقسیم می‌کند، می‌بینید، در یک سیستم ایدئال، این خطوط دقیقاً برابر با صفر هستند.

در سیستم‌های مکانیکی

نوسانگرهای جفت شده

دو جسم با جرم مساوی m را در نظر بگیرید که هر کدام به سه فنر متصل شده‌اندو هر فنر دارای ثابت فنر k هستند. از نیروی گرانش صرف نظر می‌شود. آنها سیستمی را تشکیل می‌دهند که از نظر فیزیکی متقارن است:

نقاط مرزی گیردار هستند و نمی‌توانند حرکت کنند. ما از x ₁ (t) برای نشان دادن تابع جابجایی افقی جسم (m1) سمت چپ و x ₂ (t) برای نشان دادن تابع جابجایی جرم سمت راست (m2) استفاده می‌کنیم.

اگر $\scriptstyle {\ddot {x}}$ نشانگر شتاب باشد، (مشتق دوم x (t) نسبت به زمان)، معادلات حرکت عبارتند از:

${\begin{aligned}m{\ddot {x}}_{1}&=-kx_{1}+k(x_{2}-x_{1})=-2kx_{1}+kx_{2}\\m{\ddot {x}}_{2}&=-kx_{2}+k(x_{1}-x_{2})=-2kx_{2}+kx_{1}\end{aligned}}$

از آنجایی که ما انتظار حرکت نوسانی یک حالت عادی را داریم (ω برای هر دو جسم یکسان است):

${\begin{aligned}x_{1}(t)&=A_{1}e^{i\omega t}\\x_{2}(t)&=A_{2}e^{i\omega t}\end{aligned}}$

با جایگزین کردن معادلات بالا در معادلات حرکت:

${\begin{aligned}-\omega ^{2}mA_{1}e^{i\omega t}&=-2kA_{1}e^{i\omega t}+kA_{2}e^{i\omega t}\\-\omega ^{2}mA_{2}e^{i\omega t}&=kA_{1}e^{i\omega t}-2kA_{2}e^{i\omega t}\end{aligned}}$

از آنجایی که عامل نمایی در همه جملات مشترک است، می‌توان با حذف آن، معادله را ساده کرد:

${\begin{aligned}(\omega ^{2}m-2k)A_{1}+kA_{2}&=0\\kA_{1}+(\omega ^{2}m-2k)A_{2}&=0\end{aligned}}$

و در نمایش ماتریسی:

${\begin{bmatrix}\omega ^{2}m-2k&k\\k&\omega ^{2}m-2k\end{bmatrix}}{\begin{pmatrix}A_{1}\\A_{2}\end{pmatrix}}=0$

اگر ماتریس سمت چپ وارون پذیر باشد، پاسخ یکتا پاسخ ناچیز است (A1 _, A ₂) = (x ₁ , x ₂) = (۰٬۰). پاسخ‌های مورد نظر باید برای مقادیر ω پیدا شوند که به موجب آن ماتریس سمت چپ منفرد است یعنی وارون پذیر نیست؛ بنابراین، دترمینان ماتریس باید برابر با ۰ باشد، بنابراین:

$(\omega ^{2}m-2k)^{2}-k^{2}=0$

با پیدا کردن $\omega$ ، ما دو جواب مثبت داریم:

${\begin{aligned}\omega _{1}&={\sqrt {\frac {k}{m}}}\\\omega _{2}&={\sqrt {\frac {3k}{m}}}\end{aligned}}$

با جایگزینی ω ₁ در ماتریس و حل معادله برای (A ₂ ,A _1)، (1، ۱) را دریافت می‌کنیم. اگر ω ₂ را جایگزین کنیم، (۱،۱) را دریافت می کینم. (این بردارها بردارهای ویژه هستند و فرکانس‌ها مقادیر ویژه هستند)

اولین مد نرمال به شکل زیر است:

${\vec {\eta }}_{1}={\begin{pmatrix}x_{1}^{1}(t)\\x_{2}^{1}(t)\end{pmatrix}}=c_{1}{\begin{pmatrix}1\\1\end{pmatrix}}\cos {(\omega _{1}t+\varphi _{1})}$

این مد مربوط به حرکت هر دو جرم در جهت و زمان یکسان است. این حالت را ضد متقارن می‌نامند.

مد نرمال دوم به شکل زیر است:

${\vec {\eta }}_{2}={\begin{pmatrix}x_{1}^{2}(t)\\x_{2}^{2}(t)\end{pmatrix}}=c_{2}{\begin{pmatrix}1\\-1\end{pmatrix}}\cos {(\omega _{2}t+\varphi _{2})}$

این مربوط به حرکت جسم‌ها در جهات مخالف در حالی که مرکز جرم ثابت است می‌باشد. به این مد، مد متقارن می‌گویند.

راه حل کلی، به وسیله برهم‌نهی مدهای نرمال به دست می‌آید که در آن c ₁، c ₂، φ ₁ و φ ₂ با شرایط اولیه مسئله تعیین می‌شوند.

فرآیندی که نشان داده شد را می‌توان با استفاده از فرمالیسم مکانیک لاگرانژی یا مکانیک همیلتونی تعمیم و فرمول بندی کرد.

امواج ایستاده

موج ایستاده یک شکل پیوسته از مد نرمال است. در یک موج ایستاده، تمام عناصر فضا (x , y , z) در یک فرکانس و فاز یکسان نوسان می‌کنند. در این شکل از موج نقاط با هم به نقطه تعادل می‌رسند، اما هر کدام دامنه متفاوتی دارند.

شکل کلی موج ایستاده به صورت زیر است:

$\Psi (t)=f(x,y,z)(A\cos(\omega t)+B\sin(\omega t))$

جایی که ƒ (x , y , z) نشان دهنده وابستگی دامنه به مکان است.

از نظر فیزیکی، امواج ایستاده از تداخل (برهم نهی) امواج و انعکاس آنها تشکیل می‌شوند (می توان برعکس این را هم گفت). شکل هندسی محیط تعیین می‌کند که الگوی تداخل چیست، بنابراین ƒ (x , y، z) شکل موج ایستاده را نشان می‌دهد. این وابستگی به فضا مد نرمال نامیده می‌شود.

برای مسائلی که وابستگی پیوسته به (x, y، z) دارند، هیچ مد نرمال منفرد یا محدودی وجود ندارد، بلکه بی‌نهایت مد نرمال وجود دارد. اگر مسئله مقید باشد (یعنی در بخش محدودی از فضا تعریف شده باشد) مدهای نرمال زیادی وجود خواهد داشت (معمولاً n = ۱، ۲، ۳، … شماره گذاری می‌شوند). اگر مسئله مقید نباشد، یک طیف پیوسته از مدهای نرمال وجود دارد.

جامدات الاستیک

در هر جامد دلخواه با هر دمایی، ذرات اولیه آن (مانند اتم‌ها یا مولکول‌ها) ساکن نیستند، بلکه در حول موقعیت‌های متوسط خود ارتعاش می‌کنند. ظرفیت عایق‌ها برای ذخیره انرژی حرارتی با توجه به این ارتعاشات به دست می‌آید. بسیاری از خواص فیزیکی دیگر جامد (مانند مدول الاستیسیته) را نیز می‌توان با آگاهی از فرکانس ارتعاش ذرات آن، پیش‌بینی کرد. ساده‌ترین فرض (انیشتین) این است که همه ذرات حول موقعیت‌های متوسط خود با بسامد طبیعی ν نوسان می‌کنند. این فرض را می‌توان به گونه ای دیگر توصیف کرد، همه اتم‌ها مستقل از یکدیگر با فرکانس ν ارتعاش می‌کنند. انیشتین همچنین فرض کرد که انرژی مجاز این نوسانات به حالت هارمونیک هستند. می‌توان طیف شکل موج‌ها را با استفاده از ریاضیات (مثل سری فوریه) و با استفاده از نوسانات سینوسی (یا فونون‌های حرارتی) توصیف کرد.

شش نوای اول و اصلی یک رشته ارتعاشی.

Debye تشخیص داد که هر نوسانگر همیشه به‌طور نزدیکی با نوسانگرهای کنار خود جفت شده است؛ بنابراین، دبای با جایگزین کردن نوسانگرهای جفت نشده یکسان انیشتین با همان تعداد نوسانگرهای جفت شده، ارتعاشات الاستیک یک جامد یک بعدی را با تعداد مدهای ریاضیاتی خاص ارتعاش یک تار کشیده مرتبط کرد. تون خالص کمترین پیچ یا فرکانس را پایه و مضرب‌های آن فرکانس را تون‌های هارمونیک آن فرکانس می‌نامند. دبای فرکانس ارتعاش اساسی کل بلوک جامد را به یکی از نوسانگرها اختصاص داد. دبای بالاترین فرکانسی (بین فرکانس‌های موجود) که توسط حرکت کوچک‌ترین واحد اولیه محدود می‌شود را به نوسانگرهای باقی‌مانده اختصاص داد.

به‌طور کلی مدهای نرمال ارتعاش یک کریستالی حاصل برهم‌نهی‌های بسیاری از نواهایی هستند که هر کدام دارای دامنه و فاز مناسبی می‌باشند. فونون‌های با طول موج بلندتر (فرکانس پایین) دقیقاً همان ارتعاشات صوتی هستند که در تئوری صوت مورد توجه قرار می‌گیرند. امواج طولی و عرضی از طریق جامدات منتشر می‌شوند، اما، به‌طور کلی، تنها امواج طولی توسط سیالات منتقل می‌شوند.

در مد طولی، جابجایی ذرات نسبت به موقعیت تعادل خود با جهت انتشار موج منطبق می‌باشد. امواج طولی مکانیکی را می‌توان به عنوان امواج فشاری نیز نامید. برای مدهای عرضی، ذرات منفرد عمود بر انتشار موج حرکت می‌کنند.

طبق نظریه کوانتوم، انرژی متوسط مد ارتعاشی نرمال یک جامد کریستالی با فرکانس مشخص ν برابر است با:

$E(\nu )={\frac {1}{2}}h\nu +{\frac {h\nu }{e^{h\nu /kT}-1}}$

عبارت (1/2) hν نشان دهنده «انرژی نقطه صفر» یا انرژی است که یک نوسانگر در صفر مطلق خواهد داشت.

$E(\nu )=kT\left[1+{\frac {1}{12}}\left({\frac {h\nu }{kT}}\right)^{2}+O\left({\frac {h\nu }{kT}}\right)^{4}+\cdots \right]$

با دانستن فرمول ترمودینامیک،

$\left({\frac {\partial S}{\partial E}}\right)_{N,V}={\frac {1}{T}}$

آنتروپی در هر حالت عادی است:

${\begin{aligned}S\left(\nu \right)&=\int _{0}^{T}{\frac {d}{dT}}E\left(\nu \right){\frac {dT}{T}}\\[10pt]&={\frac {E\left(\nu \right)}{T}}-k\log \left(1-e^{-{\frac {h\nu }{kT}}}\right)\end{aligned}}$

انرژی آزاد عبارت است از:

$F(\nu )=E-TS=kT\log \left(1-e^{-{\frac {h\nu }{kT}}}\right)$

که برای kT >> hν، به شکل زیر است:

$F(\nu )=kT\log \left({\frac {h\nu }{kT}}\right)$

برای محاسبه انرژی داخلی و گرما، باید تعداد مدهای ارتعاشی نرمال فرکانس بین مقادیر ν و ν + dν را بدانیم. این مقدار را f (ν)d ν در نظر بگیرید. از آنجایی که تعداد کل مدهای نرمال 3 N است، تابع f (ν) به صورت زیر به دست می‌آید:

$\int f(\nu )\,d\nu =3N$

فرایند انتگرال‌گیری در تمام فرکانس‌های کریستال انجام می‌شود. سپس انرژی داخلی U به صورت زیر به دست می‌آید:

$U=\int f(\nu )E(\nu )\,d\nu$

در مکانیک کوانتوم

مکانیک کوانتوم، حالت یک سیستم $\ |\psi \rangle$را توسط تابع موج $\ \psi (x,t)$ توصیف می‌کند. با استفاده از معادله شرودینگر، مقدار مربع قدر مطلق $\ \psi$به صورت زیر محاسبه می‌شود:

$\ P(x,t)=|\psi (x,t)|^{2}$

این معادله، چگالی احتمال اندازه‌گیری ذره در مکان x در زمان t است.

معمولاً هنگامی که نوعی از پتانسیل موجی را در بر می‌گیرد، تابع موج را می تون به یک برهم نهی از حالت‌های ویژه انرژی تجزیه کرد که هر کدام با فرکانس $\omega =E_{n}/\hbar$ نوسان می‌کنند. پس، می‌توان معادله را به صورت زیر نوشت:

$|\psi (t)\rangle =\sum _{n}|n\rangle \left\langle n|\psi (t=0)\right\rangle e^{-iE_{n}t/\hbar }$

معنای فیزیکی حالت ویژه با مبنای متعارف متفاوت است. در هنگامی که مقدار انرژی سیستم اندازه‌گیری می‌شود، تابع موج به یکی از حالت‌های ویژه خود تجزیه می‌شود بنابراین تابع موج یک ذره با حالت ویژه خالص مربوط به انرژی اندازه‌گیری شده سیستم آن توصیف می‌شود.

در زلزله‌شناسی

مدهای نرمال موجود در زمین از امواج لرزه‌ای با طول موج بلند ناشی از زمین‌لرزه‌های بزرگ ایجاد می‌شوند که باعث ایجاد امواج ایستاده می‌شوند.

یک کره الاستیک را در نظر بگیرید، برای این کره همسانگرد و همگن، مدهای کروی، حلقوی و شعاعی ایجاد می‌شود. حالت‌های کروی فقط شامل امواج P و SV (مانند امواج ریلی) می‌شوند. این حالت‌ها به شماره n و مرتبه زاویه‌ای l بستگی دارند. افزایش l شاخه‌های بنیادی موج را به سطح زمین نزدیک تر می‌کند و در مجموع به سمت امواج ریلی گرایش پیدا می‌کند. حالت‌های حلقوی موج فقط شامل امواج SH (مانند امواج لاو) هستند. حالت‌های شعاعی را می‌توان به صورت زیر مجموعه ای از حالت‌های کروی با l=۰ در نظر گرفت. این انحطاط کروی در زمین وجود ندارد زیرا با چرخش زمین، بیضی بودن و ساختار سرعت و چگالی ناهمگن سه بعدی شکسته می‌شود.

شاید فرض شود که هر مد را می‌توان جدا کرد (خود شدن تقریبی) یا اینکه بسیاری از حالت‌ها در فرکانس بسته می‌شوند (تقریب جفت متقابل). خود-کوپلینگ صرفاً سرعت فاز را تغییر می‌دهد و نه تعداد امواج اطراف یک دایره، و در نتیجه باعث کشیده شدن یا کوچک شدن الگوی موج ایستاده می‌شود. جفت متقاطع مدال به دلیل چرخش زمین، از ساختار الاستیک غیر کروی، یا به دلیل بیضی بودن زمین رخ می‌دهد و منجر به اختلاط مدهای کروی و حلقوی اساسی می‌شود.

جستارهای وابسته

• نوسان ساز هارمونیک
• سریال هارمونیک (موسیقی)
• طیف‌سنجی مادون قرمز
• تحلیل مودال
• نظریه استورم-لیوویل

منابع

• Blevins, Robert D. (2001). Formulas for natural frequency and mode shape (Reprint ed.). Malabar, Florida: Krieger Pub. ISBN 978-1-57524-184-5.
• Tzou, H.S.; Bergman, L.A., eds. (2008). Dynamics and Control of Distributed Systems. Cambridge [England]: Cambridge University Press. ISBN 978-0-521-03374-9.
• Shearer, Peter M. (2009). Introduction to seismology (2nd ed.). Cambridge: Cambridge University Press. pp. 231–237. ISBN 978-0-521-88210-1.
• Harvard lecture notes on normal modes
• https://en.wiki.x.io/wiki/Normal_mode