زاویه

زاویه^[۱] (به انگلیسی: Angle) یا گوشه یا کُنجه یکی از مفاهیم هندسه است و از برخورد دو خط مستقیم ساخته می‌شود.^[۲] یکای اندازه‌گیری زاویه درجه است که میان دو نیم‌خط که سری مشترک دارند محصور شده‌است. به سر مشترک این دو نیم‌خط رأسِ زاویه می‌گویند. بزرگی یک زاویه «مقدار چرخشی» (دورانی) است که دو نیم‌خط از گوشهٔ زاویه نسبت به یکدیگر دارند، با بدست آوردن طول کمانی پدید آمده در اثر چرخش می‌توان اندازهٔ زاویه را بدست آورد. زاویه عبارت است از شکلی که از دوران دو قطعه خط پیرامون یک نقطه پدید آید.

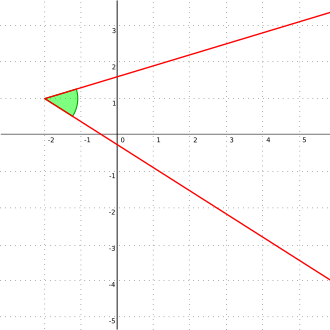
two line bent at a point — زاویهٔ سبزرنگ به‌وسیلهٔ دو نیم خط تشکیل شده‌است.

اندازه‌گیری

زاویه θ (بر حسب رادیان) برابر نسبت s به r است.

برای اندازه‌گیری زاویهٔ θ باید کمانی از دایره، که مرکز دایره بر روی راس زاویه می‌افتد را رسم کرد، برای نمونه می‌توان بوسیلهٔ پرگاری که سوزن آن بر روی راس زاویه قرار دارد یک کمان کشید، اگر طول این کمان را s بنامیم، شعاع دایرهٔ یادشده برابر با r خواهد بود و k یک عدد ثابت است که بسته به یکایی که برای اندازه‌گیری در نظر گرفته‌ایم مقدار آن تعیین می‌شود.

برای اندازه‌گیری زاویه از وسیله‌ای بنام نقاله استفاده می‌شود. توجه داشته باشید با تغییر اندازه ضلع هر زاویه اندازه آن تغییر نمی‌کند.

مقدار زاویه θ مستقل از بزرگی کمان دایره‌ای است که کشیده‌ایم چون به همان اندازه که کمان دایره بزرگ یا کوچک شود شعاع دایره نیز با همان نسبت بزرگ یا کوچک می‌شود در نتیجه s/r نسبتی همواره ثابت است.^[۳]

یکاها

روش‌های گوناگونی برای اندازه‌گیری زاویه وجود دارد که پراستفاده‌ترین آن‌ها رادیان و درجه است. به جز رادیان، دیگر یکاهای اندازه‌گیری زاویه همگی نسبتی از یک دایرهٔ کامل اند (مانند یک دور یا گرادیان). به این ترتیب یک دایره به n قسمت تقسیم شده‌است. در یکاهای مختلف، تنها مقدار n با دیگری فرق می‌کند. برای نمونه در یکای درجه n = ۳۶۰ است. مقدار $k$ که در رابطهٔ بالا گفته شد برابر است با $k={\frac {n}{2\pi }}.$ . (اثبات: رابطهٔ بالا را می‌توان به صورت $k={\frac {\theta r}{s}}.$ بازنویسی کرد. در یک دور که در آن θ برابر با n یکا است (کل یک دایره با همهٔ n قسمتش) کمانی که به آن متناظر می‌شود کل دایره‌است پس طول کمان یا s برابر با محیط دایره یا ۲πr است. با جایگذاری n برای θ و ۲πr برای s خواهیم داشت که: $k={\frac {nr}{2\pi r}}={\frac {n}{2\pi }}$ است)

دور (یا یک دایرهٔ کامل، یک چرخش یا یک گردش یا یک دایره) یک دایرهٔ کامل است. یک دور را می‌توان به صورت یکاهای صدم دور و هزارم دور نیز بیان کرد. بسته به کاربرد یک دور را با $\tau$ یا rev یا rot نیز نمایش می‌دهند؛ ولی در عبارت rpm (دور بر دقیقه) تنها حرف r نماد یک دور است. یک دور = °۳۶۰ = ۲π رادیان = چهار زاویهٔ راست‌گوشه
چارک (به انگلیسی: quadrant) برابر است با یک چهارم دور برای نمونه زاویهٔ راست یکایی است که در کتاب اصول اقلیدوس از آن استفاده شده‌است. یک چارک = °۹۰ = π/۲ rad = یک چهارم دور = ۱۰۰ gon است. در زبان آلمانی از نماد ^∟ برای نشان دادن چارک استفاده می‌کنند.
گرادیان که معادل یک چهارصدم دور است.
زاویهٔ مثلث متساوی الاضلاع برابر با ۱/۶ دور است. این یکا در گذشتهٔ دور در تمدن بابل کاربرد داشت. یکاهای درجه، دقیقهٔ یک کمان و ثانیهٔ یک کمان زیریکاهای یکای بابِلی اند. یک یکای بابلی = °۶۰ = π/۳ رادیان ≈ تقریباً ۱٫۰۴۷۱۹۷۵۵۱ رادیان

θ = s/r rad = 1 rad.

یک رادیان، زاویه‌ای است که منطبق است با کمان دایره‌ای که طول کمان با شعاع دایره برابر است (یعنی در رابطه‌ای که پیش‌تر در بالا بیان شد k = ۱ است). یک دور برابر است با ۲π رادیان و یک رادیان خود ۵۷٫۲۹۵۸ درجه یا ${\frac {180}{\pi }}.$ درجه‌است. رادیان را برای کوتاه‌تر نوشت به صورت rad نشان می‌دهند. رادیان، بی بُعد است. در بیشتر کاربردهای ریاضی به ویژه در تابع‌های مثلثاتی از رادیان استفاده می‌شود. همچنین در سامانهٔ استاندارد بین‌المللی یکاها رادیان برای نشان دادن اندازهٔ زاویه انتخاب شده‌است.
در اندازه‌گیری زاویه، به ویژه در ستاره‌شناسی یک زاویه ساعت (به انگلیسی: hour angle) برابر با ۱/۲۴ دور در نظر گرفته می‌شود. این یکا جوابگوی نیازهای ستاره‌شناسی برای یافتن محل جرم‌های آسمانی است که می‌گردند و تنها یک بار در روز از جلوی دید رد می‌شوند (مانند جای نسبی ستاره‌ها) زیریکاهای زاویه ساعت عبارتند از دقیقهٔ زمان (به انگلیسی: minute of time) و ثانیهٔ زمان (به انگلیسی: second of time). یادآوری می‌شود که این یکاها متفاوت از یکای دقیقه و ثانیهٔ کمان اند (به انگلیسی: minutes of arc) و (به انگلیسی: seconds of arc) و مقدار این زیریکاها تقریباً ۱۵ بار بزرگتر از دقیقه و ثانیهٔ کمان است. ۱ ساعت = °۱۵ = π/۱۲ رادیان = ۱/۶ چارک = ۱/۲۴ دور ≈ 16.667 gon

انواع زاویه

زاویه‌ها را با توجه به مقدارشان به این صورت طبقه‌بندی می‌کنند:

زاویه صفر: هرگاه دو ضلع برهم منطبق باشند زاویه صفر درجه بوجود می‌آید
زاویه تند: زاویه را تند یا حاده می‌گوییم هرگاه اندازه اش کمتر از ۹۰ در جه باشد.
زاویه راست: زاویه را راست یا قائم می‌گوییم هرگاه اندازه آن برابر ۹۰ در جه باشد.
زاویه باز: زاویه را باز یا منفرجه می‌گوییم هرگاه بزرگتر از ۹۰ درجه و کمتر از ۱۸۰ درجه باشد.
زاویه نیم صفحه: زاویه را نیم صفحه می‌گوییم هرگاه برابر ۱۸۰ درجه باشد.
زاویه بازتاب: زاویه را زاویه بازتاب می‌گوییم هرگاه بزرگتر از ۱۸۰ درجه و کمتر از ۳۶۰ درجه باشد.
زاویه کامل: زاویه را کامل یا تمام صفحه می‌گوییم هرگاه برابر ۳۶۰ درجه باشد.

زاویه‌های چند ضلعی‌ها

زاویهٔ داخلی(internal) و خارجی(external)

زاویه‌های خارجی زاویه‌ای که در هر رأس چند ضلعی، بین یک ضلع و امتداد ضلع دیگر تشکیل می‌شود، زاویه خارجی آن نامیده می‌شود.
زوایه‌های داخلی زاویه‌هایی که درون یک چندضلعی قرار می‌گیرند، زاویه‌های داخلی آن چند ضلعی گفته می‌شود.

انواع زوایا در دایره

زاویه محاطی

مرکزش روی محیط دایره و دو ضلع آن وترهایی از دایره هستند.

زاویه مرکزی

مرکزش روی مرکز دایره و دو ضلع آن شعاع‌هایی از دایره هستند.

نکات زوایای محاطی

همه زاویه‌های محاطی روبروی یک کمان با هم برابرند.
روبروی یک کمان می‌توان بی‌نهایت زاویه محاطی رسم کرد.
زاویه محاطی روبروی قطر دایره برابر با °۹۰ است.
اگر همه رأس‌های یک چهارضلعی روی محیط دایره قرار داشته باشند، زوایای روبروی هم مکمل یکدیگرند.^[۴]
همه زاویه‌های محاطی نصف کمان روبه رو هستند

نگارخانه

نقاله برای کشیدن زاویه، داخل شابلون

جستارهای وابسته

منابع

↑ «زاویه» [ریاضی] هم‌ارزِ «angle»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر سوم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۵۰-۸ (ذیل سرواژهٔ زاویه)
↑ Henderson, David W. ; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7.
↑ Henderson, David W. ; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7.
↑ "Angle". Wikipedia (به انگلیسی). 2022-05-04.

پیوند به بیرون

زاویه‌های دایره : زاویه محاطی و زاویه مرکزی

[1] «زاویه» [ریاضی] هم‌ارزِ «angle»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر سوم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۵۰-۸ (ذیل سرواژهٔ زاویه)

[2] Henderson, David W. ; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7.

[3] Henderson, David W. ; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7.

[4] "Angle". Wikipedia (به انگلیسی). 2022-05-04.

[۱]

[۲]

[۳]

[۴]