زاویه قائمه
در هندسه و مثلثات، یک زاویهٔ قائمه یا راستگوشه یا زاویه گونیا زاویهای است که زاویهٔ تشکیل شده بوسیلهٔ دو نیمهٔ خط راست را نیمساز میکند یعنی آن را دو قسمت برابر میکند. سخن دقیقتر آن چنین است: اگر یک نیمخط به گونهای باشد که نقطهٔ یک انتهای آن بر روی یک خط راست قرار داشته باشد و زاویههای مجاور (همسایه) آن با هم برابر باشد، آنگاه میتوان گفت که این زاویهها زاویهٔ راستاند.[۱] در چرخش (دوران)، یک زاویهٔ راست برابر است با یک چهارمِ گردش که برابر است با یک چهارم یک دایرهٔ کامل.[۲]

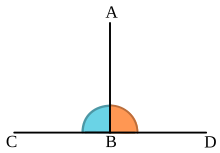
در هندسه، اگر دو خط بر یکدیگر عمود باشند آنها را عمود برهم (متعامد) میخوانیم یعنی دو خط در نقطهای که همرس شدهاند زاویهای ۹۰ درجه ساختهاند؛ و تعامد که از ویژگیهای تشکیل راستگوشه است مفهومی است که تنها در فضای برداری و برای بردارها از آن استفاده میشود. بودن یک راستگوشه در سهگوش (مثلث) باعث میشود که آن مثلث، یک مثلث راستگوشه گردد[۳] که این پدیده، پایهٔ مفهومهای به کار برده شده در مثلثات (سهبرسنجی) است.
واژه پارسی راستگوشه (rāstguše) از واژهٔ انگلیسی right angle که خود از واژهٔ لاتین angulus rectus گرته برداشته شده است. در این جا rectus بهمینوی راست و مستقیم، و angulus بهمعنی گوشه و کنجه است.
نماد
ویرایشدر یونیکد نمادهای گوناگونی برای زاویهٔ راست انتخاب شدهاست برای نمونه در U+221F نماد ∟، در U+299C نماد ⦜، در U+299D نماد ⦝ (یک کمان بر روی زاویهٔ راست همراه با یک نقطه در میانهٔ آن) به معنی زاویهٔ اندازهگیری شده، و در U+22BE همان نماد ∟ همراه با یک کمان بر روی زاویه (⊾ کمان بدون نقطه)[۴]
در شکلها، برای اینکه نشان دهند یک زاویه راست است، یک زاویهٔ راست کوچک در راس زاویه قرار میدهند تا یک مربع در گوشه تشکیل شود، گاهی به جای آن از یک کمان به همراه یک نقطه در میانهٔ آن استفاده میکنند.
اقلیدس
ویرایشدر بارهٔ زاویهٔ راست در کتاب اصول اقلیدس، کتاب ۱ تعریف ۱۰ بحث شدهاست همچنین در تعریفهای ۱۱ و ۱۲ زاویهٔ تند (برای زاویههای کوچکتر از زاویهٔ راست) و زاویهٔ باز (برای زاویههای بزرگتر از زاویه راست) تعریف شدهاند.[۵] همچنین اگر مجموع دو زاویه تشکیل یک زاویهٔ راست دهد آنها را زاویههای متمم مینامیم.[۶]
در کتابِ ۱، بُنداشتِ (اصلِ موضوعِ) ۴، پذیرفته شده بود که تمامی زاویههای راست با یکدیگر برابرند، اقلیدس از همین مطلب استفاده میکند و زاویهٔ راست را به عنوان یکای اندازهگیری دیگر زاویهها به کار میبرد. پروکلوس برای این بنداشتِ (اصل موضوعِ) اقلیدس، با استفاده از پیشفرضهای گذشته اثباتی ارائه میکند؛ اما مورد بحث قرار میگیرد که در این اثبات از بعضی فرضهای گفته نشدهاستفاده شدهاست. ساکِری هم اثباتی را ارائه میکند اما او هم در اثباتش بعضی فرضها را بدیهی در نظر گرفته و از آنها استفاده کرده بود.
دیگر یکاها
ویرایشیک زاویهٔ راست را میتوان بوسیلهٔ یکاهای مختلفی تعریف کرد:
- °۹۰ (درجه)
- ۲/π (رادیان)
- ۱۰۰ گراد (به انگلیسی grade, gradian یا gon)
- ۸ نقطه (از ۳۲ نقطهٔ صفحهٔ قطبنما)
- ۶ ساعت (زاویهساعت ستارهشناسی)
قانون ۳-۴-۵
ویرایشاعداد ۳-۴-۵ را اعداد فیثاغورسی مینامند که به آن «قانون ۳-۴-۵» نیز میگویند. گاهی برای تشخیص آنکه یک زاویه راست است یا نه، یک ضلع آن را تا ۳ واحد (برای نمونه ۳ سانتیمتر) و دیگری را ۴ واحد امتداد میدادند، آنگاه دو سر ضلعها را به هم وصل میکردند، در مثلث تشکیل شده ضلع سوم را اندازه میگرفتند، اگر ضلع سوم (ضلع بلندتر) دقیقاً ۵ واحد بود، نشان میداد که زاویه ۹۰ درجه بودهاست. مفهوم هندسی پشت این روش قضیه فیثاغورس است. («مربع وتر برابر است با مجموع مربعات دو ضلع دیگر»)
قضیه تالس
ویرایشقضیه تالس بیان میدارد که زاویهای که گوشه اش بر روی کمان دایره و دو انتهای ضلعش بر روی دو سر قطر دایره باشد (زاویه در یک نیمدایره تشکیل شده باشد) آن زاویه حتماً زاویهٔ راست است.
یادداشت و منبع
ویرایش- ↑ Wentworth صفحهٔ ۸
- ↑ Wentworth صفحهٔ ۱۱
- ↑ Wentworth صفحهٔ ۴۰
- ↑ Unicode 5.2 Character Code Charts Mathematical Operators, Miscellaneous Mathematical Symbols-B
- ↑ Heath صفحهٔ ۱۸۱
- ↑ Wentworth صفحهٔ ۹
- Wentworth, G.A. (1895). A Text-Book of Geometry. Ginn & Co.
- Euclid, commentary and trans. by توماس هیت Elements Vol. 1 (1908 Cambridge) Google Books