گراف (ساختار داده)

یک گراف^[۱] (به انگلیسی: graph) در علوم رایانه، داده‌ساختاری انتزاعی است که به صورت گراف جهت دار و بدون جهت پیاده‌سازی می‌شود و. هدفش به کارگیریِ مفهوم گراف از ریاضیات و به خصوص نظریه گراف است.

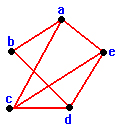
یک داده ساختار گراف اساساً از یک مجموعهٔ متناهیِ زوج‌های مرتب موسوم به یال شامل واحدهایی به نام رأس یا گره تشکیل می‌شود؛ همان‌طور که در ریاضیات به ازای یک یال (u,v) می‌گوییم که u به v می‌رود یا u و v مجاورند. همچنین می‌توان به هر یال یک گراف یک عدد نسبت داد که در این صورت گراف وزن دار به وجود می‌آید.

عملیات‌ها

عملیات ابتدایی ارائه شده توسط یک ساختار داده گراف G معمولاً شامل:^[۲]

مجاورت (G, x, y): امتحان اینکه آیا یک یال از رأس x به رأس y وجود دارد؛
همسایه‌ها (G, x):لیست تمام رأس‌ها را به طوری که یک یال از رأس x به رأس y وجود دارد؛
درج راس(G, x) :راس x را در صورت عدم وجود اضافه می‌کند؛
حذف راس (G, x) :راس x را در صورت وجود حذف می‌کند؛
درج یال (G, x, y): یک یال از رأس x به رأس y اضافه می‌کند؛
حذف یال (G, x, y): یال از رأس x به رأس y را در صورت وجود حذف می‌کند؛
گرفتن ارزش راس (G, x): مقدار مربوط به رأس x را برمی‌گرداند؛
مقداردهی راس (G, x,v) :مقدار مربوط به رأس x را v قرار می‌دهد.

در گراف وزن دار دستورهای زیر نیز وجود دارد:

گرفتن ارزش یال (G, x,y):مقدار مربوط به یال گذرنده از (x, y) را بازمی‌گرداند؛
مقدار دهی یال (G, x, y, v): مقدار مربوط به لبه (x, y) را به v تنظیم می‌کند.

نمایش گراف‌ها

ساختار داده‌های مختلفی برای نمایش گراف‌ها در عمل استفاده می‌شود:

لیست مجاورت^[۳]

راس‌ها به عنوان سوابق یا اشیا ذخیره می‌شوند و هر رأس لیستی از رأس‌های مجاور را ذخیره می‌کند. این ساختار داده‌ها اجازه ذخیره‌سازی داده‌های اضافی در رأس‌ها را می‌دهد. داده‌های اضافی را می‌توان ذخیره کرد اگر یال‌ها نیز به عنوان اشیا ذخیره شوند، در این صورت هر رأس یال‌های حادث بر خود را ذخیره می‌کند و هر یال رأس حاد خود را ذخیره می‌کند.

ماتریس مجاورت

یک ماتریس دو بعدی، که در آن ردیف‌ها نشان دهنده رأس مبدأ و ستون‌ها نشان دهنده راس مقصد هستند. داده‌ها در یال‌ها و رأس‌ها باید در خارج از ماتریس ذخیره شوند. فقط هزینه یک یال می‌تواند بین هر جفت رأس ذخیره شود.

ماتریس وقوع

یک ماتریس بولی دو بعدی، که در آن ردیف‌ها نشان دهنده رأس‌ها و ستون هانشان دهنده یال‌ها هستند. ورودی‌ها نشان می‌دهند که آیا رأس یک ردیف به یال یک ستون متصل است یا خیر.

جدول زیر، هزینه پیچیدگی زمانی را برای انجام عملیات مختلف در گراف‌ها، برای هر یک از این نمایش‌ها، | V | نشان دهنده تعداد رأس‌ها و | E | تعداد لبه هاست.


	لیست پیوندی	ماتریس مجاورت	ماتریس وقوع
ذخیره گراف	$O(\|V\|+\|E\|)$	$O(\|V\|^{2})$	$O(\|V\|\cdot \|E\|)$
درج راس	$O(1)$	$O(\|V\|^{2})$	$O(\|V\|\cdot \|E\|)$
درج یال	$O(1)$	$O(1)$	$O(\|V\|\cdot \|E\|)$
حذف راس	$O(\|E\|)$	$O(\|V\|^{2})$	$O(\|V\|\cdot \|E\|)$
حذف یال	$O(\|V\|)$	$O(1)$	$O(\|V\|\cdot \|E\|)$
سؤال: آیا رأس X و Y مجاور هستند؟ (فرض بر این است که موقعیت ذخیره‌سازی آن‌ها شناخته شده‌است)	$O(\|V\|)$	$O(1)$	$O(\|E\|)$

هر سه راه قابل اجرا برای گراف جهت دار و بدون جهت است. نمایش لیست مجاورت معمولاً ترجیح داده می‌شود چرا که یک روش فشرده برای نمایش گراف‌های کم یال فراهم می‌کند. اگر گراف متراکم یا همان پر یال باشد، نمایشِ ماتریس مجاورت مقدم است. همچنین در مواقعی که نیاز داریم سریعاً بدانیم که آیا به ازای دو رأس داده شده یال متصل‌کنندهٔ بینشان وجود دارد یا خیر، از لیست مجاورت استفاده می‌کنیم. طبقه‌بندی انواع دوگان گراف دوگان گراف‌هایی که تاکنون در علوم مختلف تعریف و استفاده شده‌اند، بر اساس نحوه استخراج به دو گروه بر مبنای گراف اولیه و مفهومی تقسیم‌بندی شده‌اند. در ادامه وجه تسمیه و مشخصات آن‌ها شرح داده شده‌اند.

این نوع دوگان گراف از گراف اولیه استخراج می‌شود. به عبارت این نوع دوگان گراف از گراف اولیه دیگر بعد از اینکه گراف اولیه بر اساس دیدگاه‌های رایج آن استخراج شد، سپس دوگان گراف آن بر اساس قوانین خاصی استخراج می‌شود. در این طبقه دو نوع دوگان یعنی دوگان گراف ورونی و دوگان گراف خطی را می‌توان گنجاند. دوگان گراف ورونی تعریف: دوگان گراف ورونی یک گراف مسطح، گرافی است که گره‌های آن نماهای گراف اولیه بوده و یال‌های آن بیانگر ارتباطات همجواری در گراف اولیه باشد این نوع دوگان دارای ویژگی‌های زیر است: -دوگان گراف ورونی یک گراف مسطح یک گراف مسطح است (که ممکن است یال موازی و حلقه نیز داشته باشد(. - اگر G یک گراف همبند وG‘، دوگان گراف ورونی آن باشد، آنگاه G نیز، دوگان گراف ورونیG‘ خواهد بود. -- دوگان‌های گراف ورونی یک گراف منحصر به فرد نیستند ویک گراف می‌تواند چندین دوگان گراف ورونی غیر یک ریخت داشته باشد. زیرا با تغییر نمایش گراف اولیه دوگان گراف ورونی آن نیز تغییر می‌کند این نوع دوگان گراف بیشتر در مسائلی که در آن‌ها نیاز به تقسیم‌بندی فضا است استفاده شده‌است. به عنوان مثال الگوریتم تولید پلیگون‌های تیسن از روی تعدا نقاط یمی از موارد کاربرد این نوع دوگان است. از دوگان ورونی گراف برای تقریب الگوریتم‌های کوتاه‌ترین مسی بر مبنای معیار فاصله استفاده کرده‌اند. چون تعداد گره‌ها در دوگان ورونی گراف به مراتب کمتر از گراف اولیه است، به همین دلیل آن‌ها نشان داده‌اند که جواب تقریبی مسئله کوتاه‌ترین مسیر بر مبنای فاصله را می‌توان در دوگان ورونی گراف اولیه محاسبه کرد.

Wallgrun^[۴] نشان داده‌است که از دوگان ورونی گراف می‌توان در مسائل طراحی حرکت رباتها استفاده برد. طراحی حرکت یک ربات در یک محدوده بسته باید بر اساس مشاهدات لحظه‌ای ربات انجام شود به نحوی که بدون برخورد با موانع و دیوارها با پیمودن کوتاه‌ترین مسیر به مقصد مورد نظر برسد. وی نشان داده‌است که ربات مورد نظر باید بر روی دوگان ورونی گراف مشاهداتش حرکت کند. وی همچنین چگونگی استخراج این دوگان ورونی گراف را بر اساس مشاهدات ربات بیان کرده‌است.^[۴]

الگوریتم‌های گراف

الگوریتم‌های گراف زمینهٔ مهم علاقه در علوم رایانه به حساب می‌آیند. برخی از عملیاتِ مربوط به گراف‌ها عبارتند از: پیدا کردن مسیری بین دو گره، مانند جستجوی عمق اول و جستجوی سطح اول و پیدا کردن کوتاهترین مسیر از یک گره به دیگری، مانند الگوریتم دیکسترا. یک روش برای پیدا کردن کوتاهترین مسیر بین هر گره و تمام گره‌های دیگر هم وجود دارد به نام الگوریتم فلوید-وارشال.

جستارهای وابسته

منابع

↑ «گراف» [ریاضی] هم‌ارزِ «graph»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر اول. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۳۱-۱ (ذیل سرواژهٔ گراف)
↑ Bowyer, A (2002-11). "LEDA—a platform for combinatorial and geometric computing Kurt Mehlhorn and Stefan Näher, Cambridge University Press, Cambridge, UK, 1999, £50 ($80), 1018 pages, [[شماره استاندارد بین‌المللی کتاب|شابک]] [[ویژه:منابع کتاب/0-521-56329-1|‎۰−۵۲۱−۵۶۳۲۹−۱]]". Computer-Aided Design. 34 (13): 1047–1048. doi:10.1016/s0010-4485(01)00159-2. ISSN 0010-4485. {{cite journal}}: Check date values in: |date= (help); URL–wikilink conflict (help)
↑ Goodrich, Michael T.; Tamassia, Roberto (2001). "Teaching internet algorithmics". Proceedings of the thirty-second SIGCSE technical symposium on Computer Science Education - SIGCSE '01. New York, New York, USA: ACM Press. doi:10.1145/364447.364561. ISBN 1-58113-329-4.
↑ ^۴٫۰ ^۴٫۱ Wallgrün، Jan Oliver (۲۰۰۹-۱۱-۱۰). Global Mapping: Minimal Route Graphs Under Spatial Constraints. Berlin, Heidelberg: Springer Berlin Heidelberg. صص. ۱۱۳–۱۴۶. شابک ۹۷۸۳۶۴۲۱۰۳۰۲۵.

توماس اچ کورمن، Charles E. Leiserson, رونالد ریوست، and کلیفورد استین (2001), "26", مقدمه‌ای بر الگوریتم‌ها (به انگلیسی) (2nd edition ed.), MIT Press and McGraw-Hill, p. 696–697 {{citation}}: |edition= has extra text (help)

[1] «گراف» [ریاضی] هم‌ارزِ «graph»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر اول. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۳۱-۱ (ذیل سرواژهٔ گراف)

[2] Bowyer, A (2002-11). "LEDA—a platform for combinatorial and geometric computing Kurt Mehlhorn and Stefan Näher, Cambridge University Press, Cambridge, UK, 1999, £50 ($80), 1018 pages, [[شماره استاندارد بین‌المللی کتاب|شابک]] [[ویژه:منابع کتاب/0-521-56329-1|‎۰−۵۲۱−۵۶۳۲۹−۱]]". Computer-Aided Design. 34 (13): 1047–1048. doi:10.1016/s0010-4485(01)00159-2. ISSN 0010-4485. {{cite journal}}: Check date values in: |date= (help); URL–wikilink conflict (help)

[3] Goodrich, Michael T.; Tamassia, Roberto (2001). "Teaching internet algorithmics". Proceedings of the thirty-second SIGCSE technical symposium on Computer Science Education - SIGCSE '01. New York, New York, USA: ACM Press. doi:10.1145/364447.364561. ISBN 1-58113-329-4.

[:0-4] ۴٫۰ ^۴٫۱ Wallgrün، Jan Oliver (۲۰۰۹-۱۱-۱۰). Global Mapping: Minimal Route Graphs Under Spatial Constraints. Berlin, Heidelberg: Springer Berlin Heidelberg. صص. ۱۱۳–۱۴۶. شابک ۹۷۸۳۶۴۲۱۰۳۰۲۵.

[۱]

[۲]

[۳]

[۴]