چهاروجهی

مقالهٔ اصلی: جسم افلاطونی

در هندسه، به یک چندوجهی که از چهار پهلوی مثلثی تشکیل شده باشد چهاروجهی می‌گویند در صورتی‌که سه وجه آن در هر گوشه به هم برسند.

چهاروجهی
رأس	4
ضلع	6
فاصله در گراف	1
فاصله در گراف	1
پیرامون	3
خودریختی‌ها	24
رنگ‌آمیزی گراف	4
ویژگی‌های	مسیر همیلتونی، گراف منتظم، symmetric، distance-regular، distance-transitive، 3-vertex-connected، گراف مسطح

چهاروجهی.

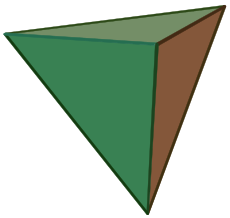
با به‌هم رسیدن سه سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع) در هر رأس، چهاروجهی منتظم تشکیل می‌شود. مجموع زوایا در هر رأس برابر ۳ × ۶۰° = ۱۸۰° می‌شود که از ۳۶۰° کمتر است، بنابراین چهاروجهی منتظم جسم افلاطونی است. اگر هریک از لیگاندها در روی هر چهار گوشه یک چهار وجهی قرار گیرد و اتم مرکزی وسط چهار وجهی قرار گیرد شکل کمپلکس چهار وجهی است.

چهاروجهی منتظم با خودش مزدوج است. یعنی با وصل کردن نقطهٔ وسط وجه‌های آن یک چهاروجهی کوچکتر می‌توان ساخت (تعداد وجوه و رئوس چهاروجهی (۴) با هم برابر است). افلاطون و فیثاغوری‌ها باور داشتند که چهاروجهی منتظم، که نوک‌های تیز دارد، ساختاردهندهٔ عنصر آتش در هستی است. کپلر باور داشت که چهاروجهی منتظم مبین فاصلهٔ بین مشتری و مریخ در منظومه شمسی است.

اطلاعات ترکیبی اجسام افلاطونی

جسم افلاطونی	تعداد وجوه (F یا q)	تعداد اضلاع (E یا p)	تعداد رئوس (V)
چهاروجهی	۴	۶	۴

بیست‌دوازده‌وجهی، که بیست وجهش مثلث متساوی‌الاضلاع و دوازده وجهش پنج‌ضلعی منتظمند، یک جسم ارشمیدسی است و می‌توان آن را با بریدن گوشه‌های دوازده‌وجهی منتظم یا بیست‌وجهی منتظم از وسط اضلاع ساخت. چهاروجهی بریده‌شده، که چهار وجهش شش‌ضلعی منتظم و چهار وجهش مثلث متساوی‌الاضلاعند نیز یک جسم ارشمیدسی است و می‌توان آن را با بریدن گوشه‌های چهاروجهی منتظم تا ۱۳ درصد طول اضلاع ساخت.

سیمپلکس تعمیم چهاروجهی منتظم در فضای n-بعدی است.

نگارخانه

• 
  پویانمایی گسترش چهاروجهی منتظم به صورت خودبرجسته‌نما. برای تماشای اثر برجسته‌نمایی تصویر در وضوح بالا و با فاصلهٔ ۳۰ تا ۵۰ سانتی‌متر از چشم مشاهده شود.
• 
• 
• 

جستار مرتبط

• تقارن چهاروجهی (گروه تقارن T)

منابع

• ویکی‌پدیای انگلیسی.
• قریب، عبدالکریم، چگونه کانی‌ها را می‌توان شناخت، تهران: ۱۳۴۴.