نیروی پایستار

یک نیروی پایستار نیرویی است که کار انجام شده توسط آن بین دو نقطه، مستقل از مسیر حرکت ذره است. به‌طور هم ارز ، یک ذره در یک حلقه بسته کار خالصی (مجموع نیروها در طول مسیر ضرب در جابه‌جایی) توسط یک نیروی پایستار انجام نمی‌دهد. نیروی گرانشی یک مثال از یک نیروی پایستار است در حالی که نیروی اصطکاک به عنوان مثالی از یک نیروی غیرپایستار شناخته می‌شود.

کار با انرژی انجام می‌شود و برخی از نیروها ویژگی‌های مشخصی دارند. یک نیروی پایستار، مانند نیروهای گرانشی که برای کار انجام شده توسط یا علیه آن تنها بستگی به نقاط شروع و پایان حرکت دارد و به مسیر طی شده بستگی ندارد. می‌توان برای هر نیروی پایستار انرژی پتانسیل تعریف کرد همان‌طور که برای نیروی گراش اینکار را انجام دادیم. برای مثال هنگامی که یک اسباب بازی، یک تایمر تخم مرغ یا یک ساعت قدیمی را خراب کنید، کاری برخلاف فنرهای ان انجان داده و در آن انرژی ذخیره می‌کنید. (فنرها ایده‌آل در نظر گرفته شده‌اند و فرض می‌شود که در آن‌ها اصطکاک و انرژی حرارتی وجود ندارد). این انرژی ذخیره شده قابل بازیابی به عنوان کار می‌باشد و خوب است که به عنوان انرژی پتانسیل موجود در فنر در نظر گرفته شود. در واقع دلیل اینکه فنر این مشخصه را دارا می‌باشد این است که نیروی آن پایستار می‌باشد. به این معنی که نیروی پایستار به انرژی پتانسیل یا ذخیره شده منتج می‌گردد. انرژی پتانسیل گرانشی یک نمونه است همان‌طور که انرژی در فنر ذخیره می‌شود. همچنین مشاهده می‌کنیم که چگونه نیروی پایستار به انرژی پایستار مربوط می‌باشد.

انرژی پتانسیل و نیروهای پایستار

انرژی پتانسیل، انرژی است که یک سیستم بسته به موقعیت، شکل یا پیکربندی دارد. انرژی ذخیره شده‌است که کاملاً قابل بازیابی باشد.

نیروی پایستار برای کارهایی که توسط یا علیه آن انجام شده تنها به نقاط ابتدایی و انتهایی حرکت بستگی دارد و به مسیر بستگی ندارد.

می‌توان انرژی پتانسیل را برای هر نیروی پایستاری تعریف کرد. کاری که بر علیه نیروی پایستار برای رسیدن به پیکربندی نهایی انجام می‌شود بستگی به پیکربندی دارد نه به روشی که انجام می‌شود و انرژی پتانسیل اضافه می‌شود.

انرژی پتانسیل یک فنر

ابتدا، یک اصطلاح برای انرژی پتانسیل در فنر تعیین کنیم (PE_s). کار لازم برای کشیدن یا فشردن فنر که از قانون هوک پیروی می‌کند در اینجا محاسبه می‌شود. (قانون هوک در الاستیسیته مورد بررسی قرار می‌گیرد: تنش و کرنش و حالت‌هایی که مقدار نیروی F در فنر و در نتیجه تغییرشکل ΔL که متناسب است نشان می‌دهد. ΔL F=K). (به شکل یک مراجعه شود)

شکل 1)

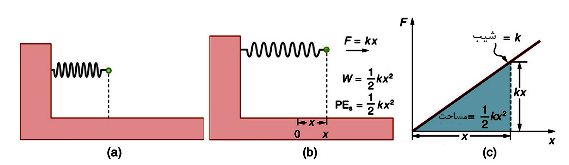
برای این فنر، ΔL (میزان تغییر شکل به وجود آمده توسط نیروی F) با فاصله x که میزان فشرده شدن یا کشیده شدن در راستای طول خود می‌باشد تعویض شده‌است؛ بنابراین نیروی لازم برای کشیدن فنر دارای مقدار F=kx، که k ثابت نیروی فنر می‌باشد. نیرو به‌طور خطی از صفر تا kx افزایش یافته تا به بیشترین موقعیت کشیده شدن برسد. میانگین نیرو kx/2 می‌باشد؛ بنابراین کار انجام شده درکشیده شدن یا فشردن فنر برابر است با:

$W_{s}=Fd=(kx/2)x=1/2kx^{2}$

در نهایت سطح زیر نمودار F-x کار انجام شده توسط نیرو می‌باشد. در شکل 1c می‌توان مشاهده کرد که این محدوده تقریباً برابر است با $1/2kx^{2}$

سپس انرژی پتانسیل فنر PE_s به صورت زیر تعریف می‌شود:

$PEs=1/2kx^{2}$

که k ثابت فنر و x تغییرمکان از موقعیت تغییرشکل نیافته می‌باشد. انرژی پتانسیل کار انجام شده روی فنر و انرژی ذخیره شده در آن تحت کشیدن یا فشردن فنر در فاصله x را نشان می‌دهد. انرژی پتانسیل فنر PE_s به مسیر بستگی ندارد. تنها به کشیده شدن یا فشرده شدن x در شکل نهایی بستگی دارد.

شکل 1) a) فنر تغییرشکل نیافته انرژی پتانسیل ذخیره شده‌ای PE_s در خود ندارد b) نیروی لازم برای کشیدن یا فشردن فنر به اندازه x مقداری برابر F=kx و کار انجام شده برای کشیدن یا فشردن برابر است با $1/2kx^{2}$.

به علت پایستار بودن نیرو، این کار به عنوان انرژی پتانسیل در فنر ذخیره شده و می‌تواند به‌طور کامل بازیابی شود. C) نمودار F-x شیبی برابر k دارد و مساحت زیر نمودار برابر می‌باشد؛ بنابراین کار انجام شده یا انرژی پتانسیل ذخیره شده برابر است با $1/2kx^{2}$

معادله $PEs=1/2kx^{2}$ اعتبار عمومی فراتر از موارد خاصی که از آنها مشتق شده دارد. انرژی پتانسیل می‌تواند در هر وسیله الاستیک با تغییرشکل دادن ذخیره شود. در واقع تعریف کلی انرژی پتانسیل، انرژی بر اساس موقعیت، شکل یا پیکربندی می‌باشد. برای تغییرشکل‌های شکل یا موقعیت، انرژی ذخیره شده برابر است با:$PEs=1/2kx^{2}$

که k در آن ثابت نیرو در سیستم مشخص و x تغییرشکل آن است.

مثال بعدی نشان داده شده در شکل ۲ برای رشته‌های گیتار می‌باشد.

پایستگی انرژی مکانیکی

شکل ۲) کار انجام شده برای تغییرشکل سیم‌های گیتار به ان انرژی پتانسیل می‌دهد. هنگامی که آزاد می‌شود، انرژی پتانسیل به انرژی جنبشی تبدیل شده و به انرژی پتانسیل توسط سیمی که به عقب و جلو نوسان می‌کند برمیگردد. مقدار بسیار کمی اصطکاک به عنوان انرژی صوتی مستهلک می‌شود که به آرامی انرژی را از رشته‌ها حذف می‌کند.

بیاید در نظر بگیریم که چه شکل از قضیه کار و انرژی اتفاق می‌افتد وقتی که تنها نیروهای پایستار مشارکت دارند. این منجر به هدایت ما به سمت قانون پایستگی انرژی می‌شود. قضیه کار و انرژی نشان می‌دهد که کار خالص انجام شده توسط تمام نیروهای وارده به سیستم برابر با تغییر در انرژی جنبشی است. به شکل معادله $Wnet=1/2mv^{2}=1/2mv0^{2}=\Delta KE$

شکل 2)

اگر تنها نیروی پایستار مؤثر باشد، سپس W_net=W_c که W_c کار کلی انجام شده توسط تمام نیروهای پایستار می‌باشد؛ بنابراین $Wc=\Delta KE$.

اکنون اگر نیروی پایستار مانند نیروی گرانشی یا نیروی فنر، کار انجام دهد، سیستم انرژی پتانسیل را از دست می‌دهد. این برابر است با $Wc=-\Delta PE$ . بنابراین $-\Delta PE=\Delta KE$ یا $\Delta KE+\Delta PE=0$ است.

این معادله به این معنی است که انرژی کلی جنبشی و پتانسیل برای هر مرحله از مشارکت نیروهای پایستار ثابت است.

فقط برای نیروهای پایستار:

$KE+PE=constant$

or

$KEi+PEi=KEf+PEf$

که i و f مقادیر ابتدایی و انتهایی را نشان می‌دهند. این معادله شکل قیه کار و انرژی برای نیروهای پایستار می‌باشد که به عنوان اصل پایستگی انرژی مکانیکی شناخته می‌شود.

به یاد داشته باشید که این‌ها به محدوده ای که تمام نیروها پاستار است اعمال می‌شود، بنابراین اصطکاک بسیار ناچیز است. انرژی جنبشی کل به علاوه انرژی پتانسیل یک سیستم به عنوان انرژی مکانیکی آن سیستم تعریف می‌شود. (KE+PE). در سیستمی که تنها نیروهای پایستار را تجربه می‌کند، انرژی پتانسیلی وجود دارد که با هر نیرو در ارتباط است و انرژی تنها از شکلی بین KE و انواع مختلف PE، با ثابت نگه داشتن انرژی کل، تغییر می‌کند.

باید توجه داشت که برای نیروهای پایستار، مستقیماً کار انجام شده آن‌ها مورد محاسبه قرار نمی‌گیرد. بلکه اثر آن‌ها بر روی انرژی پتانسیل مرتبط در نظر گرفته می‌شود. همان کاری که در مثال یک انجام شد. همچنین باید توجه داشت که مسیر طی شده را در نظر نباید گرفت فقط نقاط ابتدایی و انتهایی مهم هستند. (تا زمانی که مسیر غیرممکن باشد). این فرض معمولاً ساده‌سازی است، زیرا ممکن است مسیر پیچیده باشد و نیروها در طول مسیر ممکن است تغییر کنند.

جستارهای وابسته

• میدان برداری پایستار