منشور (هندسه)
| مجموعه منشورهای یکنواخت | |
|---|---|
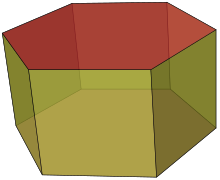 بهعنوان نمونه، یک منشور ششضلعی نشان داده شدهاست. | |
| نوع | چندوجهی یکنواخت |
| وجهها | جمعاً 2+n: ۲ n-ضلعی منتظم n مربع |
| اضلاع | 3n |
| رأسها | 2n |
| نماد شلفلی | {n}×{} یا t{2, n} |
| چیدمان رأسها | 4.4. n |
| ویژگیها | کوژ، نیمهمنتظم، رأسمتقارن |
در هندسه، یک منشور، یک چندوجهی است با یک قاعدهٔ n-ضلعی، انتقالیافتهٔ چندضلعی قاعده (در صفحهای دیگر) و n وجه دیگر که لزوماً همه متوازیالأضلاع بوده و رأسهای متناظر دو n-ضلعی را به هم متصل میکنند. همهٔ سطح مقطعهای موازی با قاعده، یکسان هستند. منشورها با توجه به تعداد اضلاع قاعدهشان نامگذاری میشوند؛ بنابراین بهعنوان مثال، یک منشور با قاعدهٔ پنجضلعی، منشور پنجضلعی نامیده میشود.
حجم و مساحت منشور
ویرایشحجم منشور اگرsمساحت قاعده و h ارتفاع باشد،حجم آن می شود:
مساحت جانبی منشور اگرpمحیط قاعده و hارتفاع باشد بر این اساس نوشته می شود.
مساحت کل منشور اگر s مساحت قاعده باشد می توان بر اساس این فرمول نوشت
تعریف
ویرایشمنشور چندوجهیای است که وجههای بالا و پایینش چندضلعیهای همنهشت (مساوی) باشند که در صفحههایی موازی هم قرار دارند. رئوس وجههای بالا و پایین یک منشور با پارهخطهایی به هم وصل میشوند. بااینحساب هر یک از وجههای جانبی منشور یک متوازیالأضلاع است و یال ایجادشده یک سطح چندوجهی است.[۱] اگر وجههای بالای منشور با خطهای عمود بر صفحهٔ شامل وجه پایینی آن به وجه پایینی وصل شده باشد، حاصل حالت خاصی از منشور موسوم به «منشور راست» است که در آن همهٔ وجههای جانبی مستطیل هستند. اگر وجوه بالا و پایین یک منشور هم مستطیل باشند منشور راست خاصی به نام مکعب مستطیل تشکیل میشود.[۱]
برای ساختن یک منشور میتوان از اکستروژن موازی بهره برد. در اکستروژن موازی رئوس چندضلعی B در صفحهٔ p در راستای خطوطی موازی کشیده میشوند.[۱]
منابع
ویرایش- ↑ ۱٫۰ ۱٫۱ ۱٫۲ Pottmann 2007, p. 76.
- مشارکتکنندگان ویکیپدیا. «Prism (geometry)». در دانشنامهٔ ویکیپدیای انگلیسی.