معادله پواسن
معادله پواسن یک معادله دیفرانسیل جزئی از نوع بیضوی در ریاضیات است که بهطور گسترده در مهندسی مکانیک و فیزیک نظری کاربرد دارد. مثلا در توصیف میدان پتانسیلی حاصل از یک بار یا چگالی جرم مشخصی ظاهر میشود ؛ برای یک میدان پتانسیلی مشخص میتوان میدان الکترواستاتیکی یا گرانشی را محاسبه کرد. این معادله تعمیم معادلات لاپلاس است که به وفور در فیزیک ظاهر میشود. این اسم به افتخار ریاضی و هندسه دان فرانسوی، سیمون دنی پواسون نامگذاری شدهاست.[۱]
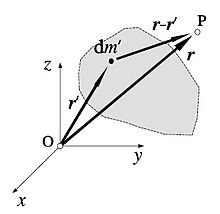
شرح معادله
ویرایشکه در آن عملگر لاپلاس است و f و φ توابعی با مقادیر حقیقی یا مختلط روی یک منیفلد هستند. معمولا f داده شده و φ خواسته میشود. وقتی منیفلد فضای اقلیدسی است ، عملگر لاپلاس بصورت ∇2 مشخص میشود بنابراین معادلهٔ پواسن عموماً به صورت زیر نوشته میشود:
در مختصات کارتزین سه بعدی، این معادله را میتوان به فرم زیر نوشت:
وقتی این همان معادله لاپلاس خواهد بود. (در واقع معادلهٔ لاپلاس حالت خاصی از معادلهٔ پواسن است ولی با توجه به اینکه حل معادلهٔ لاپلاس بسیار راحتر از معادلهٔ پواسن است، آنها را از یکدیگر تمیز میدهند)
معادلّهٔ پواسن را میتوان با استفاده از تابع گرین حل کرد.
کاربرد در الکتروستاتیک
ویرایشمسائل زیادی در الکتروستاتیک و الکترومغناطیس وجود دارند که با استفاده از این معادله توصیف میشوند. لازم است ذکر شود که در نقاطی که بار آزاد وجود ندارد معادله پواسن به معادله لاپلاس تبدیل میشود.[۲]
که در آن دیورژانس، D میدان جابجایی الکتریکی و ρf چگالی بار آزاد است.
در حالت خاصی D را میتوان به فرم زیر نوشت:
در غیاب میدان مغناطیسی متغیر، طبق قانون فارادی داریم:
که عملگر کرل و t زمان است.
جستارهای وابسته
ویرایشمنابع
ویرایش- ↑ Jackson, Julia A.; Mehl, James P.; Neuendorf, Klaus K. E., eds. (2005), Glossary of Geology, American Geological Institute, Springer, p. 503, ISBN 978-0-922152-76-6.
- ↑ فیلم آموزشی معرفی معادلات پواسون و لاپلاس،
- Poisson Equation at EqWorld: The World of Mathematical Equations.
- L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998. ISBN 0-8218-0772-2
- A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9
- Engineering Mathematics by Greenberg
- Engineerig Electromagnetics by David Cheng