فرمول هرون
در هندسه فرمول هِرون (رابطهٔ هِرون) یا دیسول هِرون (به انگلیسی: Heron's formula) فرمولی است که با بهرهگیری از آن میتوان مساحت یک مثلث را بدون داشتن ارتفاع آن به دست آورد. نام آن از نام هرون اسکندرانی گرفته شدهاست.
فرمولاسیون
ویرایشاین فرمول به صورت زیر بیان شدهاست:
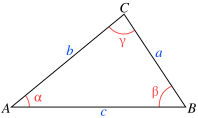
در اینجا،p برابر نصف محیط مثلث، و a و b و c برابر اضلاع مثلث و S نشانه مساحت مثلث میباشند.
فرمول هرون به روشهای زیر نیز میتواند نوشته شود
نمونه
ویرایشفرض می کنیم و
می توان صحت این فرمول و محاسبه را با استفاده از روش عادی اثبات کرد :
از آنجایی که a و b و c اعداد فیثاغورسی هستند :
b و c قائده و ارتفاع مثلث اند :
در این نمونه اندازهٔ هر ضلع مثلث به شیوهٔ عدد صحیح نوشته شدهاست، با این همه، فرمول هرون برای مثلثهایی که یک یا هر سه ضلع آن از عددهای ناصحیح و دهدهی باشد، نیز کاربرد دارد.
اثبات
ویرایشبا استفاده از جبر و قوانین نسبتهای مثلثاتی میتوان این فرمول را اثبات کرد. این اثبات با اثباتی که هرون در کتابش (متریکا) در سال ۶۰ ق. م. منتشر کرده بود، متفاوت است. مثلثی با اضلاع a و b و c در نظر میگیریم که در آن زاویه مقابل ضلع به ترتیب A و B و C است. طبق قانون کسینوسها از قانونی از کسینوسها استفاده میکنیم که به اضلاع مثلث مرتبط باشد و متغیرهای اضلاع ان مثلث دران حضور داشته باشد زیرا میخواهیم با استدلال استنتاجی از اضلاع مثلث، مساحت آن را نتیجه بگیریم و کسینوس هر زاویه برابر است با: مجموع مربعات دو ضلعی که زاویه بین ان است منهای مربع ضلع دیگر تقسیم بر؛ ۲ برابر ضرب دو ضلعی که زاویه مورد نظر بین ان دو میباشد و به بیان ریاضی داریم: ضمناً مجموع مربع سینوس یک زاویه با مربع کسینوس همان زاویه برابر است با یک و از طریق همین رابطه سینوس بر حسب مربع کسینوس بهدست میآید (رابطه دومی که در زیر ملاحظه میکنید)
- مساحت مثلث را با T نشان میدهیم. در این روش از طریق رابطه سینوس و کشیدن یک مثلث با یک ارتفاع و نوشتن رابطه مساحت مثلث یعنی قاعده ضربدر ارتفاع تقسیم بر ۲ و ادغام اینها باهم رابطه را نتیجه گرفته میشود که همان رابطه زیر است:
p یک نماد قراردادی است که همان نصف محیط مثلث است و قرار داد میشود که نصف محیط مثلث را p بنامیم پس اگر این حرف را عوض کنیم اشکال ندارد فقط باید بدانیم منظور همان نصف محیط مثلث است. ضمناً از روشهای مربع کامل سازی و اتحاد مزدوج استفاده شدهاست. همانطور که گفته شد ما میخواستیم مساحت را با استفاده از اضلاع بهدست آوریم (بدون داشتن ارتفاع) پس از قوانینی و روابطی استفاده کردیم که در بر دارنده متغیرهای اضلاع باشد یعنی در ان روابط، اضلاع مثلث وجود داشته باشد بنابراین به سراغ نسبتهای مثلثاتی و اتحادهای آنها رفتیم که به خوبی پاسخگوی نیازهای ما در قبال سوالات ریاضی در مبحث مثلثات باشد. حال شاید پرسش شما این باشد که چرا از آن اتحاد مجموع مربع سینوس و مربع کسینوس استفاده شده، در پاسخ به این سؤال باید بگویم این تنها اتحاد ساده و خوبی است که مارا در حل مسئله و ادغام روابط بالا کمک میکند و البته میشود از اتحادهای دیگر نیز کمک گرفت. این اتحاد به خوبی دو نسبت مهم و اساسی در این فرمول را پوشش میدهد و سادهتر میتوان به نتیجه رسید یعنی بدون سر در گمی و زیاد شدن محاسبات.
منابع
ویرایش- Heath, Thomas L. (1921). A History of Greek Mathematics (Vol II). Oxford University Press. pp. 321–323
- ↑ Kendig, Keith (2000). "Is a 2000-Year-Old Formula Still Keeping Some Secrets?". Amer. Math. Monthly. 107: 402–415. doi:10.2307/2695295.
برای مطالعهٔ بیشتر
ویرایش- A Proof of the Pythagorean Theorem From Heron's Formula در cut-the-knot
- Interactive applet and area calculator using Heron's Formula
- J.H. Conway discussion on Heron's Formula
- "Heron's Formula and Brahmagupta's Generalization". MathPages.com.
- A Geometric Proof of Heron's Formula
- An alternative proof of Heron's Formula without words
- Factoring Heron