ستارهگون
در ریاضیات، ستارهگون (انگلیسی: Astroid) نوع خاصی از منحنی غلتان است: یک درونچرخزاد با چهار نقطه بازگشت (تیزه). بهطور خاص، این مکان هندسی یک نقطه روی یک دایره است که در داخل یک دایره ثابت با چهار برابر شعاع غلتش میکند.[۱] با تولید مضاعف، این منحنی همچنین مکان هندسی یک نقطه روی یک دایره است که در داخل یک دایره ثابت با شعاع ۴/۳ برابر میغلتد. همچنین میتوان آن را به عنوان منحنی محاطی یک پاره خط با طول ثابت تعریف کرد که در حالی که یک نقطه انتهایی را روی هر یک از محورها نگه میدارد، حرکت میکند؛ بنابراین منحنی محاطی میله متحرک در خاگار است.

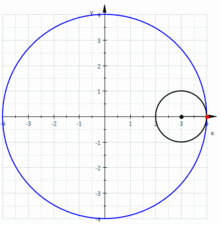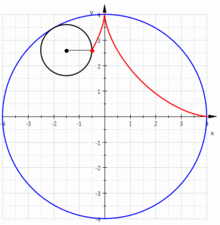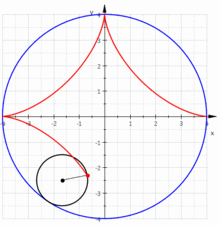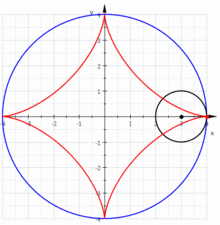
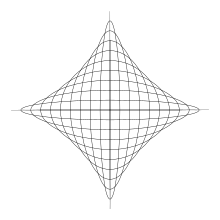
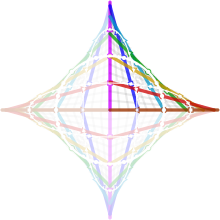
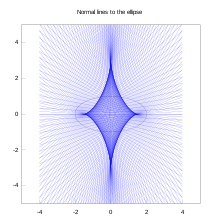
نام آستروئید از سوی یوزف یوهان فون لیترو در سال ۱۸۳۸ پیشنهاد شد.[۲][۳] این منحنی نامهای متنوعی از جمله چهارتیزهای (tetracuspid) (که هنوز هم استفاده میشود)، مکعبیچرخزادی (cubocycloid) و پاراسیکل (paracycle) داشت. شکل آن تقریباً با گسترنده یک بیضی یکسان است.
معادلات
ویرایشاگر شعاع دایره ثابت a باشد، معادله به صورت زیر داده میشود:[۴] این بدان معناست که یک ستارهگون نیز یک ابربیضی است.
معادله پارامتریها عبارتند از:
معادله پدال نسبت به مبدأ به صورت زیر است:
معادله وهول به صورت زیر است: و معادله چسارو به صورت زیر است:
دستگاه مختصات قطبی به صورت زیر است:[۵]
ستارهگون یک مکان هندسی حقیقی از یک منحنی جبری مسطح با گونای صفر است. این معادله را دارد:[۶]
بنابراین، ستارهگون یک منحنی جبری حقیقی از درجه شش است.
استخراج معادله چند جملهای
ویرایشمعادله چند جملهای را میتوان از معادله لایبنیتس با جبر مقدماتی به دست آورد:
هر دو طرف را به توان سه برسانید:
دوباره هر دو طرف را به توان سه برسانید:
اما از آنجایی که:
نتیجه میشود:
بنابراین: یا
خواص متریکی
ویرایش- مساحت محصور شده[۴]
- طول منحنی
- حجم سطح حاصل از دوران مساحت محصور شده حول محور x
- مساحت سطح حاصل از دوران حول محور x
ویژگیها
ویرایشستارهگون دارای چهار تکینگی تیزهای در صفحه حقیقی است که نقاط روی ستاره هستند. این منحنی دو تکینگی تیزهای مختلط دیگر در بینهایت و چهار نقطه دوتایی مختلط دارد که در مجموع ده تکینگی را تشکیل میدهند.
منحنی دوگان ستارهگون، منحنی چارکی با معادله است. گسترنده یک ستارهگون یک ستارهگون با دو برابر اندازه است.
ستارهگون تنها یک خط مماس در هر جهت جهتدار دارد، و آن را به یک نمونه از خارپشت تبدیل میکند.[۷]
جستارهای وابسته
ویرایشمنابع
ویرایش- ↑ Yates
- ↑ J. J. v. Littrow (1838). [[۱](https://books.google.com/books?id=AERmAAAAcAAJ&pg=PA299) "§99. Die Astrois"]. Kurze Anleitung zur gesammten Mathematik. Wien. p. 299.
{{cite book}}: Check|chapter-url=value (help) - ↑ Loria, Gino (1902). [[۲](https://archive.org/details/speziellealgebr00lorigoog) Spezielle algebraische und transscendente ebene kurven. Theorie und Geschichte]. Leipzig. pp. [۳](https://archive.org/details/speziellealgebr00lorigoog/page/n250) 224].
{{cite book}}: Check|url=value (help) - ↑ ۴٫۰ ۴٫۱ Yates, for section
- ↑ Weisstein, Eric W. "Astroid". MathWorld.
- ↑ A derivation of this equation is given on p. 3 of [۴](http://xahlee.info/SpecialPlaneCurves_dir/Astroid_dir/astroid.pdf)
- ↑ Nishimura, Takashi; Sakemi, Yu (2011). "View from inside". Hokkaido Mathematical Journal. 40 (3): 361–373. doi:10.14492/hokmj/1319595861. MR 2883496.
- J. Dennis Lawrence (1972). [[۵](https://archive.org/details/catalogspecialpl00lawr) A catalog of special plane curves]. Dover Publications. pp. 4–5, 34–35, 173–174. ISBN 0-486-60288-5.
{{cite book}}: Check|url=value (help) - Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 10–11. ISBN 0-14-011813-6.
- R.C. Yates (1952). "Astroid". A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 1 ff.
- مشارکتکنندگان ویکیپدیا. «Astroid». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۹ ژوئیه ۲۰۲۴.