روش وتری

روش وتری یکی از روش‌های یافتن ریشه معادله است. علت نام‌گذاری این روش این است که در مرحله n نقطه _n+1x از محل برخورد خط با نمودار به‌دست می‌آید. «روش وتری» مشکل اصلی که در روش نیوتن به وجود می‌آید محاسبه‌ی ${\textstyle f'(x_{n-1})}$ است. این مشکل برای توابع چند جمله‌ای مشکل زیادی به وجود نمی¬ آورد چون با توجه به الگوریتم‌های ضرب تو در تو و تقسیم ترکیبی، محاسبهٔ مشتق آنها آسان است. اما برای محاسبهٔ مشتق بیشتر توابع باید از برنامه خاصی استفاده کرد و در صورت پیچیده بودن تابع کامپیوتر باید زمان زیادی را صرف محاسبهٔ مشتق کند که هزینه بر است؛ بنابراین اگر برای مشتق، بافرض $\epsilon =x_{n-1}-x_{n-2}$ کوچک تقریبی به صورت زیر در نظر بگیریم:

$f'(x_{n-1})=\lim _{\epsilon \rightarrow 0}{\frac {f(x_{n-1})-f(x_{n-1}-\epsilon )}{\epsilon }}\approx {\frac {f(x_{n-1})-f(x_{n-2})}{x_{n-1}-x_{n-2}}}$

از بروز این مشکل جلوگیری می‌کند. این تقریب به فرمولی موسوم به روش وتری منتهی می‌شود:

$x_{n}=x_{n-1}-f(x_{n-1}){\frac {x_{n-1}-x_{n-2}}{f(x_{n-1})-f(x_{n-2})}}={\frac {x_{n-2}f(x_{n-1})-x_{n-1}f(x_{n-2})}{f(x_{n-1})-f(x_{n-2})}}.$

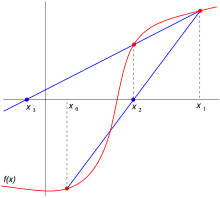
روش وتری باید با دو حدس اولیه $x_{n-1}$ و ${\textstyle x_{n-2}}$ آغاز شود. با استفاده از این دو نقطه مقادیر ${\textstyle f'(x_{n-1})}$ و ${\textstyle f(x_{n-1})}$ را محاسبه می‌کنیم. حال با استفاده از فرمول بالا نقطه جدیدx1 به وسیله درونیابی خطی بدست می‌آید. نقطه جدید نقطه ای است که ازمحل برخورد وتر حاصل از اتصال مقدار تابع در نقاط x_(0) و 〖x^'〗_۰ با محور x ها بدست می‌آید.

با یافتن نقطه جدید، نقطه ای که دارای کمترین اندیس است کنار گذاشته می‌شود. در این روش برای دنباله واگرایی امکان‌پذیر است. سرعت همگرایی این روش زمانیکه مقدار تقریب به اندازه کافی به ریشه نزدیک باشد، بیشتر از روش تکرار ساده است ولی از روش نیوتن کمتر است. و هر خطای متوالی وابسته به توانی از خطای قبلی به مانند فرمول زیر می‌باشد. e_(n+1)=k_n 〖(e_n)〗^((۱+√۵)/۲)

مزایا و ویژگی

این روش نسبت به روش نیوتن این ویژگی را دارد که به مشتق تابع نیازی ندارد. همچنین نسبت به روش نقطه ثابت، لازم نیست که دو نقطه حدس آغازین ما دو طرف ریشه تابع قرار داشته‌باشد. این روش تضمین همگرایی ندارد. اما اگر همگرا باشد، به سرعت به ریشه نزدیک می‌شود.

منابع

• محاسبات عددی «ترجمه وتالیف: دکتر خسرو مالک نژاد، دکتر اسماعیل بابلیان»