دستگاه مختصات سماوی
دستگاه مختصات سماوی، دستگاه مختصات کروی آسمان است که با آن هر نقطه یا جرمی بر متن کرهٔ آسمان توسط چند عدد مشخص میشود. در این مختصات معمولاً از تلاقی دو قوس دایره نقطهٔ مورد نظر تعیین شده و با توجه به دو مبدأ معمولاً با درجه، دقیقه و ثانیهٔ قوسی با دو مجموعه عدد توصیف میشود.
 مختصات یک ستاره در دستگاه مختصات کهکشانی، دستگاه مختصات دائرةالبروجی، و دستگاه مختصات استوایی بر روی کره آسمان. دستگاههای مختصات دائرةالبروجی و استوایی اعتدال را بهصورت جهت اولیه نشان میدهند. مختصات کهکشانی به مرکز کهکشانی اشاره دارند. مبدأ مختصات ("مرکز کره") گنگ است؛ برای اطلاعات بیشتر کره آسمان را ببینید. |
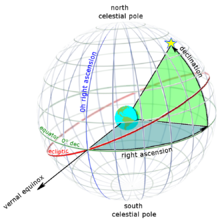
با توجه به مبدأهای متفاوت دستگاههای مختصات سماوی متمایزی (استوایی، افقی، دائرةالبروجی و کهکشانی) وجود دارند.
دستگاه مختصات استوایی
ویرایشدستگاه مختصات استوایی، مابهازای دستگاه مختصات جغرافیایی کره زمین است که دارای کاربردهای زیادی است. در این مختصات دایرهٔ استوای سماوی (یا معدلالنهار که در امتداد استوای زمین است) همراه با نیمدایرهٔ بعد حمل دو مرجع و قطبین سماوی، دو قطب یا نقاط آن هستند. معدل النهار دایره عظیمه ای است از کره سماوی، که صفحه اش بر محور عالم عمود است. مختصاتی چون میل (d) و بعد (a) از آن بدست میآید که مشابه عرض و طول جغرافیایی روی سطح زمین هستند.
بعد و میل
ویرایشمیل ستاره، قوسی است از دایره نصف النهاری واقع در مابین دایره معدل النهار و آن ستاره. اغلب در محاسبات نجومی به جای میل، فاصله قطبی ستاره را منظور میدارند. واضح است که این زاویه، متمم زاویه میل است.
بعد ستاره، عبارت از عده درجات قوسی از معدل النهار که بین صفحه نصف النهاری ستاره مفروض و صفحه نصف النهاری دیگری که مبدأ بعدها انتخاب میشود، واقع باشد. درجات این قوس از صفر تا ۳۶۰ تغییر میکند و جهت آن را خلاف جهت عقربههای ساعت میگیرند و آن را غالباً با علامت Æ نشان میدهند. تمام ستارگان واقع بر روی یک مدار، دارای یک میل و تمام نقاط یک نصف النهار دارای یک بعد میباشند؛ پس، در مقابل هر بعد و میل معین، یک نقطه وجود دارد و بالعکس.
از روی بعد و میل ستارگان میتوان به آسانی مکان هر ستاره را بر سطح یک کره مصنوعی بدست آورد. از یک نقطه اختیاری (p) واقع بر سطح کره، دایره عظیمه ای به شعاعی برابر وتر ربع محیط، با پرگار کروی رسم میکنیم. نقطه اختیاری (p) را را میتوان به منزله قطب آسمان فرض کرد. این دایره نظیر معدل النهار و نقطه متقاطر P، یعنی P' قطب جنوب است. بعد هر ستاره را میتوان به وسیله تئودولیت یا دوربین نصف النهاری تعیین کرد.[۱]
دستگاه مختصات افقی
ویرایشدستگاه مختصات افقی، که در آن افق ناظر همراه با نیمدایرهٔ سمتی شمال دو مرجع و سرسو (سمتالرأس) و پاسو (سمتالقدم)، قطبین آن شناخته میشوند. مختصات بدست آمده از آن سمت (A) و ارتفاع (a) است که هر دو به محل ناظر روی زمین و زمان بستگی دارد.
سمت و ارتفاع
ویرایشسمت ستاره، اندازه کمانی است از افق که بین دایره قائم آن ستاره و یک دایره قائم ثابت که به عنوان مبدأ اختیار میشود واقع گردد. سمت یک ستاره از صفر تا ۳۶۰ در جهت شمال به مشرق (جهت معکوس) اندازه گرفته میشود.
ارتفاع ستاره، اندازه کمانی است از دایره قائم ستاره که بین صفحه افق و آن ستاره واقع باشد. این کمان از صفر تا ۹۰ به طرف سمت الرأس اندازه گرفته میشود. سمت الرأس راصد، نقطه ای است از آسمان که در امتداد قامت شخص راصد و به طرف سر او باشد. طول یاب یا تئودولیت به ما کمک میکند که سمت و ارتفاع هر ستاره را مشخص کنیم. مسلم است که چون ارتفاع ستاره مشخص شد، فاصلة الراس نیز که متمم زاویه ارتفاع است، مشخص میشود. اگر دایره قائم تئودولیت را بر صفحه نصف النهار قرار دهیم و پیچ محور قائم آن را محکم کنیم تا دیگر به سمت راست و چپ حرکت نکند، چنین دوربینی را دوربین نصف النهاری گویند. به عبارت دیگر، میگویند دوربین را نصف النهاری کوک کردهایم.
برای این منظور، ستاره مفروض A را در موقع عبورش به نصف النهار مکان با دقت تمام رصد میکنیم. فرض میکنیم که ساعتی نجومی داشته باشیم که هنگام عبور نقطه مبدأ به نصف النهار، ساعت ۱۲ را نشان دهد. ساعت عبور ستاره A را با همین ساعت یادداشت میکنیم. اغلب همین فاصله زمانی را بعد آن ستاره گویند؛ اما، اگر بخواهیم میتوانیم آن را با محاسباتی نظیر محاسبات زیر، تبدیل به درجه کنیم:
چون خورشید در مدت شبانه روز به ظاهر یک دور به دور زمین میگردد، در هر ساعت ۱۵ درجه میپیماید. پس، میتوان طول هر مکان را نسبت به مکان دیگر از روی اختلاف ساعات حقیقی آنها بدست آورد؛ به این معنی که، هرگاه n اختلاف طول جغرافیایی و h اختلاف زمان دو مکان باشد، همواره این دستور برقرار است:
n = 15h
مثلاً هرگاه فاصله عبور نقطه γ و ستاره A به نصف النهار، ۳ ساعت و ۱۸ دقیقه و ۱۳ ثانیه باشد، داریم:
۱۵ *(ثانیه۱۳ دقیقه۱۸ ساعت۳) = Æ ۴۹° ۳۳ʹ ۱۵ ̋=
نکته: موضع هر ستاره را میتوان به کمک زاویه سمت و ارتفاع آن مشخص کرد؛ اما، این مختصات برای هر ستاره فقط در یک لحظه معین و یک افق مشخص به کار میرود و به محض اینکه راصد تغییر مکان دهد یا زمان تغییر کند، مختصات مزبور تغییر خواهد کرد. پس به دستگاه جدیدی از مختصات نیازمندیم که همیشه و در هر مکان به کار آید. این مختصات بعد و میل است.[۲]
دستگاه مختصات دائرةالبروجی
ویرایشدستگاه مختصات دائرةالبروجی، که دائرةالبروج همراه با نیمدایرهٔ مبدأ طول سماوی (متقاطع اعتدال بهاری) بعنوان دو مرجع و قطبین دائرةالبروج بعنوان دو قطب آن هستند. مؤلفههای آن عرض سماوی (b) (از مبدأ دائرةالبروج) و طول سماوی (l) هستند.
دستگاه مختصات کهکشانی
ویرایشدستگاه مختصات کهکشانی که در آن صفحه کهکشان و مرکز آن دو مرجع هستند.[۳]
جستارهای وابسته
ویرایشمنابع
ویرایش- ↑ کتاب هیئت، مؤلف سید باقرهیوی،1351
- ↑ کتاب هیئت، مؤلف سید باقرهیوی،1351
- ↑ مختصات سماوی دانشنامه ستارهشناسی
- نجوم اسلامی «مختصات سماوی» حوزه نمایندگی ولی فقیه در امور حج و زیارت
- ویکیپدیای انگلیسی