توزیع لاپلاس

در نظریه آمار و احتمالات، توزیع لاپلاس (laplace distribution)، توزیعی پیوسته است که بنام پیِر سیمون دو لاپلاس (Pierre-Simon de Laplace) نامگذاری شده. گاهی نیز توزیع نمایی دوتایی نامیده می‌شود، چراکه همانند دو توزیع نمایی که کنار همدیگر قرار داده شده‌اند، می‌ماند. جالب است بدانید این نام برخی اوقات برای خطاب توزیع گامبل نیز مورد استفاده قرار می‌گیرد.

لاپلاس

تابع چگالی احتمال
تابع توزیع تجمعی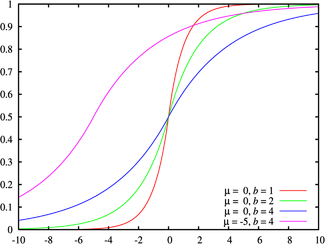
پارامترها	$\mu \,$ مکان (حقیقی) مقیاس (حقیقی) $b>0\,$
تکیه‌گاه	$x\in (-\infty ;+\infty )\,$
تابع چگالی احتمال	${\frac {1}{2\,b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,$
تابع توزیع تجمعی	see text
میانگین	$\mu \,$
میانه	$\mu \,$
مُد	$\mu \,$
واریانس	$2\,b^{2}$
چولگی	$0\,$
کشیدگی	$3\,$
آنتروپی	$\log(2\,e\,b)$
تابع مولد گشتاور	${\frac {\exp(\mu \,t)}{1-b^{2}\,t^{2}}}\,\!$ for $|t|<1/b\,$
تابع مشخصه	${\frac {\exp(\mu \,i\,t)}{1+b^{2}\,t^{2}}}\,\!$

این توزیع به بیان ساده، نمایانگر تفاوت دو متغیر تصادفی مستقل که از توزیع نمایی پیروی می‌کنند، می‌باشد.

کاربرد معمول این توزیع، برای مدل کردن نمونه‌هایی است که آرام تر از توزیع نمایی به صفر میل می‌کنند ( یا به عبارت آماری از توزیع دم سنگین پیروی می‌کنند).

به طور مثال افزایش جنبش لاپلاس یا پراکندگی عملیات گاما که در یک مقیاس زمانی اندازه‌گیری می‌شود، از توزیع لاپلاس پیروی می‌کنند.

خصوصیات

تابع چگالی احتمال

تابع چگالی احتمال توزیع لاپلاس با پارامترهای μ و b:

$={\frac {1}{2b}}\left\{{\begin{matrix}\exp \left(-{\frac {\mu -x}{b}}\right)&{\text{if }}x<\mu \\[8pt]\exp \left(-{\frac {x-\mu }{b}}\right)&{\text{if }}x\geq \mu \end{matrix}}\right.$$f(x\mid \mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,\!$

در اینجا، $\mu$یک پارامتر مکانی است و b>۰، که برخی اوقات به عنوان انحراف بیان می‌شود، یک پارامتر مقیاس است. اگر $\mu =0$ و $b=1$، نیم خط مثبت دقیقاً یک توزیع نمایی با مقیاس ۱/۲ خواهد بود.

تابع چگالی احتمال لاپلاس همچنین یادآور توزیع نرمال است؛ گرچه، برخلاف توزیع نرمال که براساس مجذور اختلاف با میانگین ($\mu$) بیان می‌شود، چگالی لاپلاس براساس قدر مطلق تفاضل از میانگین بیان می‌گردد. در نتیجه، توزیع لاپلاس دنباله بزرگتری از توزیع نرمال دارد.

تابع توزیع تجمعی

توزیع لاپلاس برای انتگرال‌گیری راحت است (با توجه به تقارن توزیع) بخاطر وجود تابع قدرمطلق. تابع توزیع تجمعی آن به صورت زیر است:

${\begin{aligned}F(x)&=\int _{-\infty }^{x}\!\!f(u)\,\mathrm {d} u={\begin{cases}{\frac {1}{2}}\exp \left({\frac {x-\mu }{b}}\right)&{\mbox{if }}x<\mu \\1-{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{if }}x\geq \mu \end{cases}}\\&={\tfrac {1}{2}}+{\tfrac {1}{2}}\operatorname {sgn}(x-\mu )\left(1-\exp \left(-{\frac {|x-\mu |}{b}}\right)\right).\end{aligned}}$

تابع وارون تجمعی آن همانند زیر است:

$F^{-1}(p)=\mu -b\,\operatorname {sgn}(p-0.5)\,\ln(1-2|p-0.5|).$

نکته: در زبان R، می‌توانید از توابع rlaplace, dlaplace, plaplace, qlaplace برای محاسبه مقادیر بالا و تولید داده‌های نمونه از این توزیع استفاده کنید.

توزیع لاپلاس با متغیرهای ۴ و ۰.۵

توجه داشته باشید که شکل این توزیع بسته به پارامتر های مکان و مقیاس تعیین می‌شود.

در شکل کنار صفحه، یک مثال با پارامترهای ۴ و ۰.۵ به نمایش درآمده است.

امید ریاضی و واریانس

امید ریاضی و واریانس تقریباً شبیه به توزیع نرمال بوده با تفاوتی کوچک:

$E(X)=\mu$

$var(X)=2\sigma ^{2}$

تولید متغیر تصادفی بر اساس توزیع لاپلاس

اگر متغیر تصادفی $U$ از توزیع یکنواخت در بازه $\left(-1/2,1/2\right]$را داشته باشیم، متغیر تصادفی

$X=\mu -b\,\operatorname {sgn}(U)\,\ln(1-2|U|)$

از توزیع لاپلاس با پارامترهای $\mu$ و $b$پیروی می‌کند. این متغیر از روی تابع وارون تجمعی که در بالا به آن اشاره شد، بدست می‌آید.

متغیر تصادفی توزیع ${\textrm {Laplace}}(0,b)$می‌تواند از روی تفاضل دو متغیر تصادفی از توزیع نمایی ${\textrm {Exponential}}(1/b)$نیز بدست بیاید. همچنین، ${\textrm {Laplace}}(0,1)$نیز از لگاریتم نرخ دو متغیر تصادفی توزیع یکنواخت نیز پدید بیاید.

در R کافیست از تابع rlaplace استفاده کرد و با تعیین تعداد نمونه مورد نیاز و پارامتر های مکان و مقیاس، نمونه تصادفی مورد نیاز را ایجاد کنیم.

تخمین پارامتر

برای بدست آوردن برآورد درست‌نمایی بیشینه (MLE) کافیست مثل هر توزیع دیگری احتمال داشتن N نمونه از توزیع یکسان و مستقل از هم $x_{1},x_{2},...,x_{N}$، که قبلاً مشاهده نموده‌ایم را با توجه به رابطه تئوری و گذاشتن متغیر مجهول به جای پارامتر مطلوب، را بیشینه کنیم. برای اینکار کافیست از رابطه به دست آمده مشتق بگیریم و آن را برابر صفر قرار دهیم.

بعد از انجام محاسبات به فرمول زیر می‌رسیم:

${\hat {b}}={\frac {1}{N}}\sum _{i=1}^{N}|x_{i}-{\hat {\mu }}|$

( برآورد درست‌نمایی بیشینه (MLE) ${\hat {\mu }}$از $\mu$میانهٔ نمونه‌ها است، و برآورد درست‌نمایی بیشینه ${\hat {b}}$از $b$میانگین قدر مطلق انحراف از میانه است )

(نشانگر ارتباط توزیع لاپلاس و حداقل انحراف مطلق است)

نمونه‌ای در R

به طور مثال نمونه‌ای از کد لازم برای ترسیم توزیع را در R در زیر قرار داده‌ایم.

cl <- rainbow(10)
plots <- ggplot()
for(j in 1:6){
  sample <- seq(from=0, to=10, by=.1)
  p <- dlaplace(sample, j, j)
  plots <- plots + geom_line(data.frame(x=sample, y=p), mapping = aes(x=x, y=y), color=cl[j])
}
print(plots)

تاریخچه

از این توزیع غالباً به عنوان اولین قانون خطاهای لاپلاس شناخته می‌شود. او این قانون را در سال ۱۷۷۴ زمانی که متوجه شد تکرار خطاها می‌تواند به شکل تابعی نمایی از اندازه‌اش، وقتی که علامت آن مورد توجه نگیرد، بیان شود، منتشر نمود. جالب است بدانید که این توزیع از قدیمی ترین توزیع‌های مطرح شده است، اما کمتر استفاده‌ای از آن می‌شود.

کینز مقاله‌ای بر پایهٔ پایان نامهٔ قبلی خود در سال ۱۹۹۱ منتشر نمود که در آن نشان داد توزیع لاپلاس انحراف از معیار را کمینه می‌کند.

منابع

• ویکی‌پدیای انگلیسی
• http://www.math.wm.edu/~leemis/chart/UDR/PDFs/ExponentialLaplace.pdf
• https://www.statisticshowto.datasciencecentral.com/laplace-distribution-double-exponential/
• http://mathworld.wolfram.com/LaplaceDistribution.html