تغییر شکل (فیزیک)

تغییر شکل (به انگلیسی: Deformation) در مکانیک محیط‌های پیوسته، تبدیل یک بدنه از یک پیکربندی مرجع به پیکربندی فعلی است.^[۱] پیکربندی مجموعه‌ای است که همهٔ موقعیت‌های مکانی ذره‌های آن بدنه را شامل می‌شود.

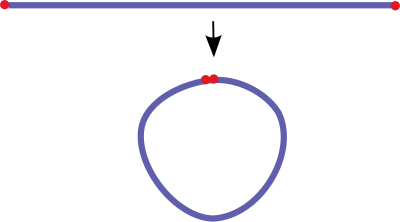
تغییر شکل ممکن است در اثر بارهای خارجی،^[۲] نیروهای بدنه (مانند نیروهای گرانش یا الکترومغناطیسی) یا تغییر دما، میزان رطوبت، یا واکنش‌های شیمیایی و غیره ایجاد شود.

کرنش توصیف تغییر شکل از نظر جابجایی نسبی ذرات در بدنه است که حرکات بدن سفت و محکمی را حذف می‌کند. بسته به اینکه آیا با توجه به پیکربندی اولیه یا نهایی بدن و اینکه آیا تانسور متریک یا دوتایی آن در نظر گرفته شده‌است، ممکن است گزینه‌های معادل متفاوتی برای بیان یک میدان کرنش ایجاد شود.

در یک جسم پیوسته، یک میدان تغییر شکل، که ناشی از یک میدان تنش است، در اثر نیروهای وارده یا به دلیل برخی تغییرات در میدان دمای بدنه به وجود می‌آید. رابطه بین تنش و کرنش با معادلات سازنده، به عنوان مثال، قانون هوک برای مواد الاستیک خطی بیان می‌شود. تغییر شکل هایی که پس از حذف میدان تنش از بین می روند، تغییر شکل الاستیک نامیده می شوند. در این حالت، زنجیره به‌طور کامل پیکربندی اصلی خود را بازیابی می‌کند. از طرف دیگر، تغییر شکل‌های بازگشت‌ناپذیر حتی پس از برطرف شدن تنش‌ها باقی می‌مانند. یک نوع تغییر شکل برگشت‌ناپذیر تغییر شکل پلاستیک است، که در اجسام مادی بعد از رسیدن تنش به مقدار مشخصی به نام حد الاستیک یا تنش تسلیم ایجاد می‌شود و نتیجه لغزش یا مکانیسم‌های نابجایی در سطح اتمی است. نوع دیگری از تغییر شکل برگشت‌ناپذیر تغییر شکل ویسکوز است که قسمت برگشت‌ناپذیر تغییر شکل ویسکوالاستیک است.

در صورت تغییر شکل الاستیک، عملکرد پاسخی که کرنش را با تنش تغییر شکل‌ پیوند می‌دهد، تانسور سازگاری مواد است.

کرنش

کرنش نشان دهنده جابجایی بین ذرات در بدنه نسبت به طول مرجع است. تغییر شکل یک جسم به شکل x = F(X) بیان می‌شود، که X موقعیت مرجع نقاط مادی بدنه است. چنین معیاری بین حرکات صلب بدن (انتقال و چرخش) و تغییر شکل (اندازه) بدن تمایز قائل نمی‌شود. یک تغییر شکل دارای واحدهای طول است.

برای مثال می‌توانیم strain را تعریف کنیم. ${\boldsymbol {\varepsilon }}\doteq {\cfrac {\partial }{\partial \mathbf {X} }}\left(\mathbf {x} -\mathbf {X} \right)={\boldsymbol {F}}'-{\boldsymbol {I}}$ در رابطه بالا، I ماتریس همانی است. کرنش‌ها بدون بعد هستند و معمولاً به صورت ده‌دهی، درصد یا به صورت قسمت در نماد (بخش در یکای سنجش) بیان می‌شوند. کرنش‌ها اندازه‌گیری می‌کنند که تغییر شکل داده‌ شده چقدر با تغییر شکل جسم صلب تفاوت دارد.^[۳]

کرنش به طور کلی یک کمیت تانسوری است. بینش فیزیکی در مورد کرنش ها را می توان با مشاهده اینکه یک کرنش معین می تواند به اجزای عادی و برشی تجزیه شود، به دست آورد. مقدار کشش یا فشار در امتداد عناصر خط مادی یا الیاف‌ها، کرنش معمولی است، و میزان اعوجاج مرتبط با لغزش لایه‌های صفحه بر روی یکدیگر، کرنش برشی در یک جسم در حال تغییر شکل است.^[۴] این تغییرات را می توان با ازدیاد طول، کوتاه شدن، یا تغییرات حجم، یا اعوجاج زاویه ای اعمال کرد.^[۵]

در صورت افزایش طول خط ماده، کرنش معمولی را کرنش کششی و در غیر این صورت، اگر کاهش یا فشار در طول خط ماده ایجاد شود، به آن کرنش فشاری می گویند.

اندازه‌گیری‌های کرنش

بسته به میزان کرنش یا تغییر شکل موضعی، تحلیل تغییر شکل به سه نظریه تقسیم می‌شود:

نظریه کرنش محدود که نظریه کرنش بزرگ یا نظریه تغییر شکل بزرگ نیز نامیده می‌شود، به تغییر شکل‌هایی می‌پردازد، که در آن هر دو چرخش و کرنش خودسرانه بزرگ هستند.در این حالت، پیکربندی‌های تغییر شکل نیافته و تغییر شکل‌یافته، برای مواد مکانیک محیط‌های پیوسته به طور قابل‌توجهی متفاوت هستند و باید بین آنها تمایز واضحی قائل شد. این امر معمولاً در مورد الاستومرها، مواد تغییر شکل یافته پلاستیک و سایر مایعات و بافت نرم بیولوژیکی صادق است.

نظریه کرنش بینهایت کوچک، که به آن نظریه کرنش کوچک، نظریه تغییر شکل کوچک، نظریه جابجایی کوچک یا نظریه شیب جابجایی کوچک نیز گفته می‌شود، که در آن کرنش‌ها و چرخش‌ها هر دو کوچک هستند. در این حالت، پیکربندی‌های تغییر شکل نیافته و تغییر شکل یافته بدنه را می‌توان یکسان فرض کرد. نظریه کرنش بینهایت کوچک، در تجزیه و تحلیل تغییر شکل موادی که رفتار کشسانی دارند، مانند موادی که در کاربردهای مکانیکی و مهندسی عمران یافت می‌شوند، استفاده می‌شود، برای مثال بتن و فولاد.

تئوری جابجایی بزرگ یا چرخش بزرگ، که کرنش های کوچک اما چرخش ها و جابجایی های بزرگ را فرض می کند.

در هر یک از این نظریه‌ها، کرنش به طور متفاوتی تعریف می‌شود. کرنش مهندسی رایج‌ترین تعریفی است، که برای مواد مورد استفاده در مهندسی مکانیک و سازه به کار می‌رود، که در معرض تغییر شکل‌های بسیار کوچکی هستند. از سوی دیگر، برای برخی از مواد، به عنوان مثال، الاستومرها و پلیمرها، که در معرض تغییر شکل‌های بزرگ قرار می‌گیرند، تعریف مهندسی کرنش قابل اجرا نیست، به عنوان مثال، کرنش‌های مهندسی معمولی بیشتر از 1%^[۴]. بنابراین تعاریف پیچیده‌تری از کرنش مورد نیاز است، مانند کشش، کرنش لگاریتمی، Green strain و Almansi strain.

کرنش مهندسی

کرنش مهندسی که به عنوان کرنش کوشی (Cauchy strain) نیز شناخته می‌شود، به صورت نسبت تغییر شکل کل به بعد اولیه جسم مادی که نیرو بر آن اعمال می‌شود، بیان می‌شود. کرنش نرمال مهندسی یا کرنش کششی مهندسی یا کرنش اسمی e، مربوط به یک عنصر خط ماده یا فیبری که به صورت محوری بارگذاری شده است، به صورت تغییر طول ΔL در واحد طول L اصلی عنصر خط یا الیاف بیان می‌شود. اگر الیاف مواد کشیده شوند، کرنش طبیعی، مثبت و در صورت فشرده شدن منفی است. بنابراین، داریم: $e={\frac {\Delta L}{L}}={\frac {l-L}{L}}$ e کرنش نرمال مهندسی است، L طول اصلی فیبر و l طول نهایی فیبر است. اندازه‌گیری کرنش اغلب در قسمت‌های در میلیون (per million) یا microstrains بیان می‌شود.

کرنش برشی واقعی به عنوان تغییر زاویه (بر حسب رادیان) بین دو عنصر خط مادی، که در ابتدا عمود بر یکدیگر در پیکربندی تغییر شکل نیافته یا اولیه هستند، تعریف می‌شود. کرنش برشی مهندسی به عنوان مماس آن زاویه تعریف می‌شود و برابر است با طول حداکثر تغییر شکل تقسیم بر طول عمود در صفحه اعمال نیرو، که گاهی اوقات محاسبه آن را آسان می‌کند.

نسبت کشش

نسبت کشش یا نسبت گسترش معیاری از کرنش کششی یا نرمال یک عنصر خط دیفرانسیل است، که می‌تواند در پیکربندی تغییر شکل نیافته یا پیکربندی تغییر شکل یافته تعریف شود. این پارامتر به عنوان نسبت بین طول نهایی l و طول اولیه L خط ماده تعریف می‌شود. $\lambda ={\frac {l}{L}}$ نسبت گسترش تقریباً به کرنش مهندسی مربوط می شود. $e={\frac {l-L}{L}}=\lambda -1$ این معادله بیانگر این است که کرنش نرمال صفر است، به طوری که وقتی کشش برابر با واحد است، تغییر شکلی وجود ندارد. نسبت کشش در تجزیه و تحلیل موادی استفاده می‌شود، که تغییر شکل‌های بزرگی را نشان می‌دهند، مانند الاستومرها، که می‌توانند نسبت کشش 3 یا 4 را قبل از شکست حفظ کنند. از سوی دیگر، مواد مهندسی سنتی، مانند بتن یا فولاد، در نسبت کشش بسیار کمتری شکست می‌خورند.

کرنش واقعی

کرنش لگاریتمی (ε) که به آن کرنش واقعی یا کرنش هنکی (Hencky strain) نیز می‌گویند.^[۶] با در نظر گرفتن یک کرنش افزایشی (لودویک):

$\delta \varepsilon ={\frac {\delta l}{l}}$ کرنش لگاریتمی با ادغام این کرنش افزایشی به دست می‌آید: ${\begin{aligned}\int \delta \varepsilon &=\int _{L}^{l}{\frac {\delta l}{l}}\\\varepsilon &=\ln \left({\frac {l}{L}}\right)=\ln(\lambda )\\&=\ln(1+e)\\&=e-{\frac {e^{2}}{2}}+{\frac {e^{3}}{3}}-\cdots \end{aligned}}$ e کرنش مهندسی است. کرنش لگاریتمی اندازه گیری صحیح کرنش نهایی را زمانی که تغییر شکل در یک سری از افزایش‌ها انجام می‌شود، با در نظر گرفتن تأثیر مسیر کرنش ارائه می دهد.^[۴]

کرنش گرین (Green strain)

کرنش گرین به صورت زیر تعیین می‌شود:

$\varepsilon _{G}={\tfrac {1}{2}}\left({\frac {l^{2}-L^{2}}{L^{2}}}\right)={\tfrac {1}{2}}(\lambda ^{2}-1)$ کرنش آلمانسی (Almansi strain)

کرنش اویلر-آلمانسی به این صورت تعریف می‌شود:

$\varepsilon _{E}={\tfrac {1}{2}}\left({\frac {l^{2}-L^{2}}{l^{2}}}\right)={\tfrac {1}{2}}\left(1-{\frac {1}{\lambda ^{2}}}\right)$

کرنش نرمال و برشی

کرنش‌ها به دو دسته نرمال یا برشی طبقه‌بندی می‌شوند. یک کرنش عمودی، بر روی سطح یک المان عمود است و یک کرنش برشی موازی با سطح المان است. این تعاریف با تعاریف تنش نرمال و تنش برشی سازگار است.

کرنش نرمال

برای یک ماده همسانگرد که از قانون هوک پیروی می‌کند، یک تنش عمودی، باعث کرنش عمودی می‌شود. کرنش‌های معمولی باعث اتساع می‌شوند.

عنصری مستطیلی دو بعدی، بینهایت کوچک، با ابعاد $dx \times dy$ را در نظر بگیرید که پس از تغییر شکل، به شکل لوزی در می‌آید. تغییر شکل با میدان جابجایی $u$ توصیف می شود. از هندسه شکل مجاور داریم:

به‌علاوه، می‌توانید توضیح مختصری را نیز در پایین قاب اضافه کنید.

تغییر شکل هندسی دو بعدی یک عنصر بینهایت کوچک

$\mathrm {length} (AB)=dx$

و همچنین:

${\begin{aligned}\mathrm {length} (ab)&={\sqrt {\left(dx+{\frac {\partial u_{x}}{\partial x}}dx\right)^{2}+\left({\frac {\partial u_{y}}{\partial x}}dx\right)^{2}}}\\&={\sqrt {dx^{2}\left(1+{\frac {\partial u_{x}}{\partial x}}\right)^{2}+dx^{2}\left({\frac {\partial u_{y}}{\partial x}}\right)^{2}}}\\&=dx~{\sqrt {\left(1+{\frac {\partial u_{x}}{\partial x}}\right)^{2}+\left({\frac {\partial u_{y}}{\partial x}}\right)^{2}}}\end{aligned}}$

برای شیب های جابجایی بسیار کوچک، مربع های مشتق از $u_{y}$ و $u_{x}$ ، ناچیز هستند و داریم:

$\mathrm {length} (ab)\approx dx\left(1+{\frac {\partial u_{x}}{\partial x}}\right)=dx+{\frac {\partial u_{x}}{\partial x}}dx$ کرنش نرمال در جهت $x$ برای عنصر مستطیلی به صورت زیر تعریف می‌شود:

$\varepsilon _{x}={\frac {\text{extension}}{\text{original length}}}={\frac {\mathrm {length} (ab)-\mathrm {length} (AB)}{\mathrm {length} (AB)}}={\frac {\partial u_{x}}{\partial x}}$

به طور مشابه، کرنش نرمال در جهت‌های $y$ و $z$ به صورت زیر تعریف می‌شود: $\varepsilon _{y}={\frac {\partial u_{y}}{\partial y}}\quad ,\qquad \varepsilon _{z}={\frac {\partial u_{z}}{\partial z}}$

کرنش برشی

کرنش برشی مهندسی ( $\gamma _{xy}$ ) به عنوان تغییر زاویه بین خطوط AC و AB تعریف می‌شود. از این رو، $\gamma _{xy}=\alpha +\beta$ از هندسه شکل، داریم: ${\begin{aligned}\tan \alpha &={\frac {{\tfrac {\partial u_{y}}{\partial x}}dx}{dx+{\tfrac {\partial u_{x}}{\partial x}}dx}}={\frac {\tfrac {\partial u_{y}}{\partial x}}{1+{\tfrac {\partial u_{x}}{\partial x}}}}\\\tan \beta &={\frac {{\tfrac {\partial u_{x}}{\partial y}}dy}{dy+{\tfrac {\partial u_{y}}{\partial y}}dy}}={\frac {\tfrac {\partial u_{x}}{\partial y}}{1+{\tfrac {\partial u_{y}}{\partial y}}}}\end{aligned}}$

برای شیب‌های جابجایی کوچک داریم: ${\frac {\partial u_{x}}{\partial x}}\ll 1~;~~{\frac {\partial u_{y}}{\partial y}}\ll 1$ برای چرخش‌های کوچک، یعنی $α$ و $β$ که کوچکتر از 1 هستند، ما $tan α \approx α$ ، $tan β \approx β$ را داریم. از این رو،

$\alpha \approx {\frac {\partial u_{y}}{\partial x}}~;~~\beta \approx {\frac {\partial u_{x}}{\partial y}}$

بنابراین $\gamma _{xy}=\alpha +\beta ={\frac {\partial u_{y}}{\partial x}}+{\frac {\partial u_{x}}{\partial y}}$ با مبادله $x$ و $y$ و $u x$ و $u y$ می‌توان نشان داد $γ xy = γ yx$ .

به طور مشابه، برای صفحات $yz$ و $xz$ ، ما داریم: $\gamma _{yz}=\gamma _{zy}={\frac {\partial u_{y}}{\partial z}}+{\frac {\partial u_{z}}{\partial y}}\quad ,\qquad \gamma _{zx}=\gamma _{xz}={\frac {\partial u_{z}}{\partial x}}+{\frac {\partial u_{x}}{\partial z}}$ سپس اجزای کرنش برشی کششی تانسور کرنش بینهایت کوچک را می‌توان با استفاده از تعریف کرنش مهندسی، $γ$ ، بیان کرد.

${\underline {\underline {\boldsymbol {\varepsilon }}}}={\begin{bmatrix}\varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{yy}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{zz}\\\end{bmatrix}}={\begin{bmatrix}\varepsilon _{xx}&{\tfrac {1}{2}}\gamma _{xy}&{\tfrac {1}{2}}\gamma _{xz}\\{\tfrac {1}{2}}\gamma _{yx}&\varepsilon _{yy}&{\tfrac {1}{2}}\gamma _{yz}\\{\tfrac {1}{2}}\gamma _{zx}&{\tfrac {1}{2}}\gamma _{zy}&\varepsilon _{zz}\\\end{bmatrix}}$

تانسور متریک

یک میدان کرنش مرتبط با جابجایی، در هر نقطه، با تغییر در طول بردارهای مماس که نشان‌دهنده سرعت منحنی‌های پارامتری دلخواه از آن نقطه هستند، تعریف می‌شود. یک نتیجه هندسی اساسی، بر اساس عقیده فرشه (Fréchet)، بیان می‌کند، که اگر طول بردارهای مماس، بدیهیات و قانون متوازی‌الاضلاع را برآورده کنند، طول آن بردار جذر مقدار فرم درجه دوم آن است، که با فرمول پلاریزاسیون با یک نقشه دوخطی قطعی مثبت به نام تانسور متریک همراه است.

توضیح تغییر شکل

تغییر شکل تغییر در خواص متریک یک جسم پیوسته است، به این معنی که منحنی رسم شده در محل قرارگیری اولیه بدنه زمانی که به منحنی در مکان نهایی جابجا شود، طول خود را تغییر می‌دهد. اگر هیچ یک از منحنی‌ها تغییر طول ندهد، می‌گویند که یک جابجایی جسم صلب رخ داده است.

شناسایی یک پیکربندی مرجع یا حالت هندسی اولیه بدنه پیوسته که تمام پیکربندی‌های بعدی از آن ارجاع می‌شوند، راحت است. نیازی نیست که بدنه از پیکربندی مرجع پیروی کند. اغلب، پیکربندی در $t = 0$ به عنوان پیکربندی مرجع، $κ 0 (B)$ در نظر گرفته می‌شود. پیکربندی در زمان فعلی t پیکربندی فعلی است.

رای تجزیه و تحلیل تغییر شکل، پیکربندی مرجع به عنوان پیکربندی تغییر شکل نیافته و پیکربندی فعلی به عنوان پیکربندی تغییر شکل یافته شناسایی می‌شود. علاوه بر این، هنگام تجزیه و تحلیل تغییر شکل، زمان در نظر گرفته نمی‌شود، بنابراین دنباله‌ای از پیکربندی‌ها بین پیکربندی‌های تغییر‌شکل‌ نیافته و تغییر شکل‌یافته هیچ اهمیتی ندارد.

اجزای $X i$ بردار موقعیت $X$ یک ذره در پیکربندی مرجع، با توجه به سیستم مختصات مرجع، ماده یا مختصات مرجع نامیده می‌شوند. از طرف دیگر، اجزای $x i$ بردار موقعیت $x$ یک ذره در پیکربندی تغییر شکل یافته، با توجه به سیستم مختصات مکانی مرجع، مختصات فضایی نامیده می‌شوند.

دو روش برای تجزیه و تحلیل تغییر شکل یک پیوستار وجود دارد. یک توصیف بر حسب مختصات مادی یا ارجاعی انجام می‌شود که توصیف مادی یا توصیف لاگرانژی نامیده می‌شود. توصیف دوم تغییر شکل از نظر مختصات فضایی انجام می‌شود که توصیف فضایی یا توصیف اویلری نامیده می‌شود.

در هنگام تغییر شکل یک جسم پیوسته تداوم وجود دارد به این معنا که:

نقاط مادی که در هر لحظه یک منحنی بسته را تشکیل می‌دهند همیشه در هر زمان بعدی یک منحنی بسته را تشکیل می‌دهند.

نقاط مادی که در هر لحظه یک سطح بسته را تشکیل می‌دهند، همیشه در هر زمان بعدی یک سطح بسته را تشکیل می‌دهند و ماده درون سطح بسته همیشه درون آن باقی می‌ماند.

تغییر شکل آفین

اگر بتوان آن را با تبدیل آفین توصیف کرد، تغییر شکل را تغییر شکل آفین می‌نامند. چنین تبدیلی از یک تبدیل خطی (مانند چرخش، برش، گسترش و فشرده‌سازی) و یک انتقال جسم صلب تشکیل شده است. به تغییر شکل‌های آفین، تغییر شکل‌های همگن نیز می‌گویند.

بنابراین، یک تغییر شکل آفین شکل دارد. $\mathbf {x} (\mathbf {X} ,t)={\boldsymbol {F}}(t)\cdot \mathbf {X} +\mathbf {c} (t)$ که در آن $x$ موقعیت یک نقطه در پیکربندی تغییر شکل یافته، $X$ موقعیت در پیکربندی مرجع، $t$ پارامتری شبیه زمان، $F$ ترانسفورماتور خطی و $c$ ترجمه است. در فرم ماتریسی، که در آن اجزاء بر اساس یک مبنای متعارف هستند.

${\begin{bmatrix}x_{1}(X_{1},X_{2},X_{3},t)\\x_{2}(X_{1},X_{2},X_{3},t)\\x_{3}(X_{1},X_{2},X_{3},t)\end{bmatrix}}={\begin{bmatrix}F_{11}(t)&F_{12}(t)&F_{13}(t)\\F_{21}(t)&F_{22}(t)&F_{23}(t)\\F_{31}(t)&F_{32}(t)&F_{33}(t)\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\end{bmatrix}}+{\begin{bmatrix}c_{1}(t)\\c_{2}(t)\\c_{3}(t)\end{bmatrix}}$ اگر $F = F (X, t)$ یا $c = c (X, t)$ تغییر شکل فوق غیر آفین یا ناهمگن می‌شود.

حرکت بدنه‌ی صلب

حرکت جسم صلب یک تغییر شکل آفین خاص است، که شامل هیچ گونه برش، امتداد یا فشار نمی‌شود. ماتریس تبدیل F، تعامد مناسبی است، تا اجازه چرخش را بدهد اما بازتابی نداشته باشد.

یک حرکت بدنه صلب را می توان به صورت زیر توصیف کرد: $\mathbf {x} (\mathbf {X} ,t)={\boldsymbol {Q}}(t)\cdot \mathbf {X} +\mathbf {c} (t)$

به‌طوریکه ${\boldsymbol {Q}}\cdot {\boldsymbol {Q}}^{T}={\boldsymbol {Q}}^{T}\cdot {\boldsymbol {Q}}={\boldsymbol {\mathit {1}}}$

به بیان ماتریسی ${\begin{bmatrix}x_{1}(X_{1},X_{2},X_{3},t)\\x_{2}(X_{1},X_{2},X_{3},t)\\x_{3}(X_{1},X_{2},X_{3},t)\end{bmatrix}}={\begin{bmatrix}Q_{11}(t)&Q_{12}(t)&Q_{13}(t)\\Q_{21}(t)&Q_{22}(t)&Q_{23}(t)\\Q_{31}(t)&Q_{32}(t)&Q_{33}(t)\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\end{bmatrix}}+{\begin{bmatrix}c_{1}(t)\\c_{2}(t)\\c_{3}(t)\end{bmatrix}}$

جستارهای وابسته

منابع

↑ Truesdell, C.; Noll, W. (2004). The non-linear field theories of mechanics (3rd ed.). Springer. p. 48.
↑ Wu, H. -C. (2005). Continuum Mechanics and Plasticity. CRC Press. ISBN 1-58488-363-4.
↑ Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5. Archived from the original (PDF) on 2010-03-31.
↑ ^۴٫۰ ^۴٫۱ ^۴٫۲ Rees, David (2006). Basic Engineering Plasticity: An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. ISBN 0-7506-8025-3. Archived from the original on 2017-12-22.
↑ "Earth."Encyclopædia Britannica from Encyclopædia Britannica 2006 Ultimate Reference Suite DVD .[2009].
↑ Hencky, H. (1928). "Über die Form des Elastizitätsgesetzes bei ideal elastischen Stoffen". Zeitschrift für technische Physik. 9: 215–220.

پیوند به بیرون

[Truesdell-1] Truesdell, C.; Noll, W. (2004). The non-linear field theories of mechanics (3rd ed.). Springer. p. 48.

[wu-2] Wu, H. -C. (2005). Continuum Mechanics and Plasticity. CRC Press. ISBN 1-58488-363-4.

[3] Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5. Archived from the original (PDF) on 2010-03-31.

[:0-4] ۴٫۰ ^۴٫۱ ^۴٫۲ Rees, David (2006). Basic Engineering Plasticity: An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. ISBN 0-7506-8025-3. Archived from the original on 2017-12-22.

[5] "Earth."Encyclopædia Britannica from Encyclopædia Britannica 2006 Ultimate Reference Suite DVD .[2009].

[6] Hencky, H. (1928). "Über die Form des Elastizitätsgesetzes bei ideal elastischen Stoffen". Zeitschrift für technische Physik. 9: 215–220.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]